题目内容
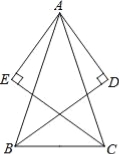
【题目】如图，在△ABC中，AB=AC，BD平分∠ABC，CE平分∠ACB，过点A分别作BD、CE的垂线段AD、AE，垂足为D、E，求证：AD=AE．
【答案】证明参见解析.
【解析】
试题分析：根据等边对等角可得∠ABC=∠ACB，再根据角平分线的定义求出∠ABD=∠ACE，然后利用“角角边”证明△ABD和△ACE全等，根据全等三角形对应边相等证明即可．
试题解析：∵AB=AC，∴∠ABC=∠ACB，∵BD平分∠ABC，CE平分∠ACB，∴∠ABD=
∠ABC，∠ACE=∠ACB，∴∠ABD=∠ACE，∵过点A分别作BD、CE的垂线段AD、AE，垂足为D、E，∴∠D=∠E=90°，在△ABD和△ACE中，，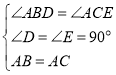
,∴△ABD≌△ACE（AAS），∴AD=AE．
练习册系列答案
相关题目
【题目】在一次实验中，小明把一根弹簧的上端固定，在其下端悬挂物体，下面是测得的弹簧的长度y与所挂物体的质量x的一组对应值：
所挂重量x（kg） | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧长度y（cm） | 18 | 20 | 22 | 24 | 26 | 28 |
（1）上述反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
（2）写出y与x之间的关系式，并求出当所挂重物为6kg时，弹簧的长度为多少？
