题目内容
【题目】阅读下面的例题及点拨,并解决问题:
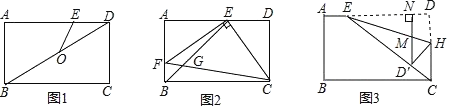
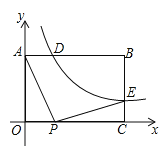
例题:如图①,在等边![]() 中,
中,![]() 是
是![]() 边上一点(不含端点
边上一点(不含端点![]() ),
),![]() 是
是![]() 的外角
的外角![]() 的平分线上一点,且
的平分线上一点,且![]() .求证:
.求证:![]() .
.

点拨:如图②,作![]() ,
,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,得等边
,得等边![]() ,连接
,连接![]() .易证:
.易证:![]() ,可得
,可得![]() ;又
;又![]() ,则
,则![]() ,可得
,可得![]() ;由
;由![]() ,进一步可得
,进一步可得![]() 又因为
又因为![]() ,所以
,所以![]() ,即:
,即:![]() .
.

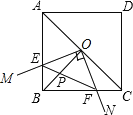
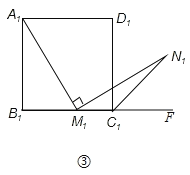
问题:如图③,在正方形![]() 中,
中,![]() 是
是![]() 边上一点(不含端点
边上一点(不含端点![]() ),
),![]() 是正方形
是正方形![]() 的外角
的外角![]() 的平分线上一点,且
的平分线上一点,且![]() .求证:
.求证:![]() .
.
【答案】见解析;
【解析】
延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() ,则
,则![]()
![]() ,得出
,得出![]() 是等腰直角三角形,由等腰直角三角形的性质得出
是等腰直角三角形,由等腰直角三角形的性质得出![]() ,证出
,证出![]() ,得出
,得出![]() ,三点共线,由
,三点共线,由![]() 证明
证明![]() 得出
得出![]() ,得出
,得出![]() ,由等腰三角形的性质得出
,由等腰三角形的性质得出![]() ,证出
,证出![]() ,得出
,得出![]() ,即可得出结论.
,即可得出结论.
解:延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() ,如图所示:
,如图所示:
则![]() ,
,![]()
![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∵![]() 是正方形
是正方形![]() 的外角
的外角![]() 的平分线上一点,
的平分线上一点,
∴![]() ,
,
∴![]() ,
,
∴![]() ,三点共线,
,三点共线,
在![]() 和
和![]() 中,
中,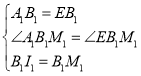 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目