题目内容
如图，AB、AC是⊙O的弦，OE⊥AB、OF⊥AC，垂足分别为E、F．如果EF=3.5，那么BC=________．
7
分析：由OE垂直于AB，利用垂径定理得到E为AB的中点，同理得到F为AC的中点，可得出EF为三角形ABC的中位线，利用三角形的中位线定理得到BC=2EF，即可求出BC的长．
解答：∵OE⊥AB，OF⊥AC，
∴E为AB的中点，F为AC的中点，即EF为△ABC的中位线，
∴EF=
BC，又EF=3.5，
则BC=2EF=7．
故答案为：7
点评：此题考查了垂径定理，以及三角形的中位线定理，熟练掌握定理是解本题的关键．
分析：由OE垂直于AB，利用垂径定理得到E为AB的中点，同理得到F为AC的中点，可得出EF为三角形ABC的中位线，利用三角形的中位线定理得到BC=2EF，即可求出BC的长．
解答：∵OE⊥AB，OF⊥AC，
∴E为AB的中点，F为AC的中点，即EF为△ABC的中位线，
∴EF=
BC，又EF=3.5，则BC=2EF=7．
故答案为：7
点评：此题考查了垂径定理，以及三角形的中位线定理，熟练掌握定理是解本题的关键．
练习册系列答案
相关题目
D交OB的延长线于点D．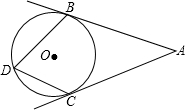
如图，AB、AC是⊙O的切线，且∠A=54°，则∠BDC=
如图，AB，AC是圆的两条弦，AD是圆的一条直径，且BC⊥AD，下列结论中不一定正确的是（ ）
如图，AB和AC是等腰△ABC的两腰，CD和BE是两腰上的高，CD和BE相交于点F．