题目内容
【题目】如图1,在平面直角坐标系中,A(-2,0),C(2,2),过C作CB⊥x轴于B.



(1)如图1,则三角形ABC的面积
(2)如图2,若过B作BD∥AC交y轴于D,则∠BAC+∠ODB的度数为
如图2,若AE,DE分别平分∠CAB,∠ODB,求∠AED的度数.
(3)在坐标轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等,若存在,求出P点坐标;若不存在,请说明理由.
【答案】(1)4; (2)90° (3) 存在,在X轴上为(-6,0), 在y轴上为(0,3)和(0,-1)
【解析】分析:(1)先利用CB⊥x轴确定C点坐标,然后根据三角形面积公式求解;(2)连结AD,如图2,根据平行线的性质由BD∥AC得到∠BAC=∠ABD,然后利用∠OBD+∠ODB=90°即可得到∠BAC+∠ODB=90°;根据角平分线定义得∠EAO=![]() ∠BAC,∠EDO=
∠BAC,∠EDO=![]() ∠ODB,则可计算出∠EAO+∠EDO=
∠ODB,则可计算出∠EAO+∠EDO=![]() (∠BAC+∠ODB)=45°,接着根据三角形内角和定理可计算出∠AED=45°.
(∠BAC+∠ODB)=45°,接着根据三角形内角和定理可计算出∠AED=45°.
(3)如图3由OA=OB得到OQ=![]() BC=1,则Q点坐标为(0,1),设P点坐标为(0,t),根据三角形面积公式得到
BC=1,则Q点坐标为(0,1),设P点坐标为(0,t),根据三角形面积公式得到![]() ×2×|t-1|+
×2×|t-1|+![]() ×2×|t-1|=4,然后解绝对值方程得到t的值,从而确定P点坐标.
×2×|t-1|=4,然后解绝对值方程得到t的值,从而确定P点坐标.
本题解析:
(1) ∵C(2,2),CB⊥x轴于B,∴C点坐标为(2,0),
∴三角形ABC的面积=![]() ×2×(2+2)=4;
×2×(2+2)=4;
(2)
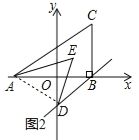
解:过E作EF∥AC,∴∠CAE=∠AEF
∵BD∥AC,∴BD∥EF,∴∠FED=∠BDE
∵AE,DE分别平分∠CAB,∠ODB
∴∠CAE=![]() ∠CAB ∠BDE =
∠CAB ∠BDE =![]() ∠BDO
∠BDO
∴∠AED=∠AEF+∠FED=∠CAE+∠BDE=![]() ∠CAB+
∠CAB+![]() ∠BDO =
∠BDO =![]() (∠CAB+∠BDO)=45° (3)在X轴上为(-6,0),
(∠CAB+∠BDO)=45° (3)在X轴上为(-6,0),
在y轴上为(0,3)和(0,-1) 。
