题目内容
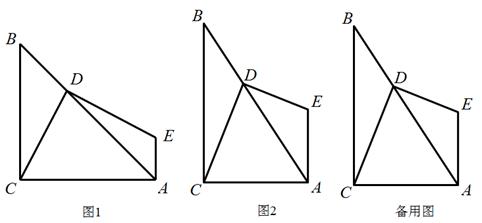
探究一:如图1,已知正方形ABCD,E、F分别是BC、AB上的两点,且AE⊥DF.小明经探究,发现AE=DF.请你帮他写出证明过程.
探究二:如图2,在矩形ABCD中,AB=3,BC=4,E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE⊥FH.小明发现,GE与FH并不相等,请你帮他求出 的值.
的值. 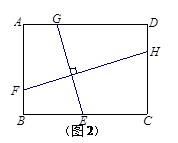
探究三:小明思考这样一个问题:如图3,在正方形ABCD中,若E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE=FH,试问:GE⊥FH是否成立?若一定成立,请给予证明;若不一定成立,请画图并作出说明.
(1)证明见解析;
(2)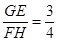 ;
;
(3)不一定成立,图形见解析.
解析试题分析:(1)证明AE=DF,只要证明三角形ABE和DAF全等即可.它们同有一个直角,且AB=AD,又因为∠AEB=90°﹣∠BAE=∠AFD,这样就构成了全等三角形判定中的AAS,两三角形就全等了;
(2)作GM⊥BC于M,FN⊥CD于N,再由GE⊥FH,可得△GME∽△FNH,根据相似性质即可;
(3)不一定成立.
试题解析:(1)∵DF⊥AE,
∴∠AEB=90°﹣∠BAE=∠AFD,
又∵AB=AD,∠ABE=∠DAF=90°,
∴△ABE≌△DAF,
∴AE=DF;
(2)作GM⊥BC于M,FN⊥CD于N,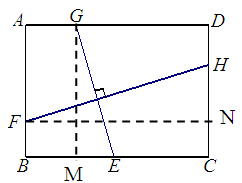
∵GE⊥FH
∴∠MGE=∠NFH,
∴△GME∽△FNH.
∴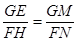 .
.
∵AB=GM=3,FN=BC=4,
∴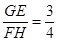 ;
;
(3)不一定成立,如图:
当GE=FH时,GE和FH位置不确定,只有GE=FH=AD时,GE⊥FH.
考点:1.正方形的性质,2.三角形相似.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 ,DE=2,求AD的长.
,DE=2,求AD的长.
 是
是 上一点,
上一点, ∥
∥ ,
, 分别交
分别交 于点
于点 ,∠1=∠2,探索线段
,∠1=∠2,探索线段 之间的关系,并说明理由.
之间的关系,并说明理由.
 .
.
 ,在同一时刻测得小丽和建筑物
,在同一时刻测得小丽和建筑物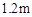 和
和 ,求建筑物
,求建筑物
 .求证:DE∥BC
.求证:DE∥BC

