题目内容
小明对直角三角形很感兴趣. △ABC中,∠ACB=90°,D是AB上任意一点,连接DC,作DE⊥DC,EA⊥AC,DE与AE交于点E.请你跟着他一起解决下列问题: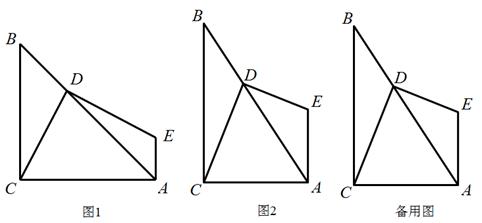
(1)如图1,若△ABC是等腰直角三角形,则DE,DC有什么数量关系?请给出证明.
(2)如果换一个直角三角形,如图2,∠CBA=30°,则DE,DC又有什么数量关系?请给出证明.
(3)由(1)、(2)这两种特殊情况,小明提出问题:如果直角三角形ABC中,BC=mAC,那DE, DC有什么数量关系?请给出证明.
(1)DE=DC,证明见解析;(2)DC=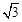 DE,证明见解析;(2)DC=
DE,证明见解析;(2)DC=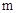 DE,证明见解析.
DE,证明见解析.
解析试题分析:(1) 过点D作DF⊥AC,DG⊥AE于点G,通过证明△CDF≌△EDG而得出结论;
(2) 过点D作DF⊥AC,DG⊥AE于点G,应用锐角三角函数定义和.特殊角的三角函数值,通过证明△CDF∽△EDG而得出结论;
(3) 过点D作DF⊥AC,DG⊥AE于点G,根据BC=mAC,通过证明△CDF∽△EDG而得出结论.
试题解析:(1)DE=DC,证明如下:
如图,过点D作DF⊥AC,DG⊥AE于点G,
由EA⊥AC可知四边形AGDF为矩形,∴DG="FA."
∵DF∥BC,△ABC是等腰直角三角形,∴DF=AF,即DG=DF.
又∵DE⊥DC,∴∠CDE-∠EDF=∠FDG-∠EDF,即∠CDF=∠EDG.
∴△CDF≌△EDG. ∴DE=DC.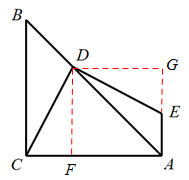
(2)DC=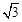 DE,证明如下:
DE,证明如下:
如图,过点D作DF⊥AC,DG⊥AE于点G,
由EA⊥AC可知四边形AGDF为矩形,∴DG=FA.
∵DE⊥DC,∴∠CDE-∠EDF=∠FDG-∠EDF,即∠CDF=∠EDG. ∴△CDF∽△EDG. ∴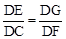 .
.
又∵△ADF∽△ABC,∴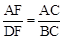 .
.
∵∠CBA=30°,∴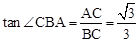 .
.
∴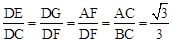 .∴DC=
.∴DC=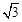 DE.
DE.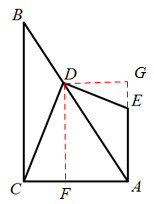
(3) DC=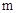 DE.证明如下:
DE.证明如下:
如图,过点D作DF⊥AC,DG⊥AE于点G,
由EA⊥AC可知四边形AGDF为矩形,∴DG=FA.
∵DE⊥DC,∴∠CDE-∠EDF=∠FDG-∠EDF,即∠CDF=∠EDG. ∴△CDF∽△EDG. ∴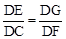 .
.
又∵△ADF∽△ABC,∴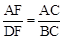 .
.
∵BC=mAC,∴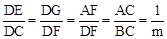 .∴DC=
.∴DC=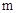 DE.
DE.
考点:1.矩形的判定和性质;2. 等腰直角三角形的性质;3.全等三角形的判定和性质;4.锐角三角函数定义;5.特殊角的三角函数值;6.相似三角形的判定和性质.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案 ∠BAF,AF=
∠BAF,AF= AD,请你判断线段FM和FN之间的数量关系,并证明你的判断是正确的.
AD,请你判断线段FM和FN之间的数量关系,并证明你的判断是正确的.

 :
: ,求证:
,求证: .
.

 的值.
的值. 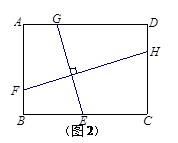


 的长.(提示:请先在备用图中画出相应的图形,再求
的长.(提示:请先在备用图中画出相应的图形,再求
 =_______;
=_______;
 角(
角( ),其他条件不变,判断
),其他条件不变,判断
 ,点N在线段OD上,且NO=3.点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.
,点N在线段OD上,且NO=3.点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.
 ,
, 时,
时, 与
与 的大小关系是_________________.
的大小关系是_________________. ,
, 时,
时, 为圆O的内接三角形,
为圆O的内接三角形, 为直径,过C作
为直径,过C作 于D,设
于D,设 ,BD=b.
,BD=b.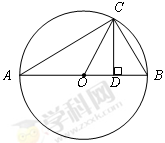
 表示线段OC,CD;
表示线段OC,CD;

