Question

【题目】如图，点是正方形对角线的延长线上任意一点，以线段 为边作一个正方形，线段和相交于点．

(1)求证：；

(2)判断与的位置关系，并说明理由；

Answer 1

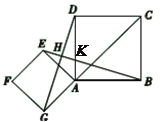
【答案】(1)证明见解析； (2)，理由见解析.

【解析】

（1）由四边形EFGA和四边形ABCD是正方形，易证得△GAD≌△EAB，即EB=GD；

（2）EB⊥GD，由（1）得∠ADG=∠ABE则在△DHK中，∠DHK=90°所以EB⊥GD；

(1)∵四边形ABCD是正方形

∴AB=AD, ∠DAB=90°

∵四边形AEFG是正方形

∴AE=AG, ∠EAG=90°

∴∠DAB=∠EAG

∴∠DAB+∠EAD=∠EAG+∠EAD

即∠BAE=∠DAG

∴

∴

(2)

理由如下：

∵

∴∠ABE=∠ADG

∵∠ABE+∠AKB=90°

∴ ∠ADG+∠AKB=90°

∵∠AKB=∠DKH

∴∠ADG+∠DKH=90°

∴∠DHK=90°

即.