题目内容
【题目】(1) ;(2)
;(2) .
.
【答案】(1)![]() ;(2)
;(2) .
.
【解析】
试题(1)由第2个方程可得,y=2(x+1)-11③,把③代入第1个方程消去未知数y,解得x值,再把x值代入③解得y的值;
(2)根据方程组中各未知数的系数的特点,把三个方程的左右两边分别相加,得到x+y+z=1,把x+y=1-z代入①解得z值,把x+z=1-y代入②解得y值,把y+z=1-x代入③解得x值.
试题解析:解:(1)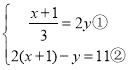 ,
,
由②得y=2(x+1)-11③,
把③代入①,得:![]() ,
,
解得x=5,
把x=5代入③,得:y=2(5+1)-11=1,
所以方程组的解为![]() .
.
(2) ,
,
①+②+③得:x+y+z=1,
所以x+y=1-z④,x+z=1-y⑤,y+z=1-x⑥,
把④代入①解得z=-2,
把⑤代入②解得y=-5,
把⑥代入③解得x=8,
所以方程组的解为 .
.

练习册系列答案
相关题目




