Question

【题目】如图，PA、PB是⊙O的切线，CD切⊙O于点E，△PCD的周长为12，∠APB=60°．

求：（1）PA的长；

（2）∠COD的度数．

Answer 1

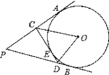
【答案】.解：（1）由切线长定理可得△PCD的周长=PA+PB,PA=PB,

∴PA=PB=6 ………………………………………(4分)

(2)连接OA、OB、OE

利用切线长定理可证∠COD=∠AOB=（180°-∠P）=60° ………… (8分)

【解析】

(1)、可通过切线长定理将相等的线段进行转换，得出三角形PDE的周长等于PA+PB的结论，即可求出PA的长；(2)、根据三角形的内角和求出∠ADC和∠BEC的度数和，然后根据切线长定理，得出∠EDO和∠DEO的度数和，再根据三角形的内角和求出∠DOE的度数．

(1)∵CA，CE都是⊙O的切线，∴CA＝CE， 同理：DE＝DB，PA＝PB，

∴△PCD的周长＝PD＋CD＋PC＝PD＋PC＋CA＋BD＝PA＋PB＝2PA＝12，即PA的长为6；

(2)∵∠P＝60°，∴∠PCE＋∠PDE＝120°， ∴∠ACD＋∠CDB＝360°－120°＝240°，

∵CA，CE是⊙O的切线， ∴∠OCE＝∠OCA＝∠ACD； 同理：∠ODE＝∠CDB，

∴∠OCE＋∠ODE＝ (∠ACD＋∠CDB)＝120°， ∴∠COD＝180－120°＝60°.