题目内容
【题目】探索发现
(1)数学课上,老师出了一道题:如图①,在Rt△ABC中,∠C=90°,∠A=22.5°,请你在图①中,构造一个合适的等腰直角三角形,并求出tan22.5°的值(结果可带根号);
学以致用
(2)如图②,厂房屋顶人字架(AB=BD)的跨度为10米(即AD=10米),∠A=22.5°,BC是中柱(C为AD的中点),请运用(1)中的结论求中柱BC的长(结果可带根号).

【答案】(1)![]() -1(2)中柱BC的长为(5
-1(2)中柱BC的长为(5![]() -5)米
-5)米
【解析】试题分析: (1)在AC上截取CE=BC=x,结合等腰直角三角形的性质以及利益锐角三角函数关系得出答案;
(2)利用(1)中所求,由tan22.5°=![]() 1=
1=![]() ,进而得出BC的长.
,进而得出BC的长.
试题解析:
(1)设BC=x,在AC 上截取CE=BC=x,连接BE.
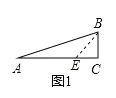
∵∠C=90°,
∴∠BEC=45°.
∵∠A=22.5°,
∴∠ABE=22.5°,
∴AE=BE=![]() x,
x,
∴AC=![]() x+x,
x+x,
∴tan22.5°=![]() =
=![]() -1.
-1.
(2)∵AB=BD,
∴△ABD为等腰三角形.
∵C为AD的中点,
∴AC=CD=5米,BC⊥AD.
在Rt△ABC中,BC=AC·tan22.5°=(5![]() -5)米.
-5)米.
答:中柱BC的长为(5![]() -5)米.
-5)米.
点睛: 此题主要考查了解直角三角形的应用,正确正确做出辅助线是解题关键.

练习册系列答案
相关题目

