题目内容
一辆汽车匀速通过某段公路，所需时间t（h）与行驶速度v（km/h）满足函数关系：
，其图象为如图所示的一段曲线，且端点为
和
，若行驶速度不得超过60（km/h），则汽车通过该路段最少需要时间为（ ）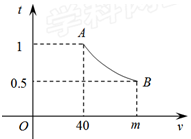
A． 分 | B．40分 | C．60分 | D． 分 |
B
解析试题分析：把点A（40，1）代入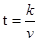
，求得k的值，再把点B代入求出的解析式中，求得m的值，然后把v＝60代入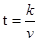，求出t的值即可．
解：由题意得，函数经过点（40，1），
把（40，1）代入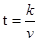，得k＝40，
则解析式为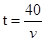
，再把（m，0.5）代入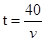，得m＝80；
把v＝60代入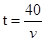，得
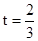，小时＝40分钟，
则汽车通过该路段最少需要40分钟；
故选B．
考点：反比例函数的应用．
练习册系列答案
教材全解字词句篇系列答案
相关题目
下列点位于反比例函数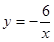
图象上的是
| A．（2，3） | B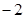．（ ，3） | C．（3，2） | D．（ ） |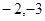
如图，△AOB为等边三角形，点A在第四象限，点B的坐标为（4，0），过点C（
4，0）作直线l交AO于D，交AB于E，且点E在某反比例函数
图象上，当△ADE和△DCO的面积相等时，k的值为（ ）
A． | B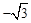． | C． | D． |
双曲线
与直线y=2x+1的一个交点横坐标为﹣1，则k=（ ）
| A．﹣2 | B．﹣1 | C． 1 | D．2 |
若反比例函数经过点（1,2），则下列点也在此函数图象上的是（ ）
| A．（1，-2） | B．（-1，﹣2） | C．（0，﹣1） | D．（﹣1，﹣1） |
（k≠0）上．将正方形沿x轴负方向平移a个单位长度后，点C恰好落在该双曲线上，则a的值是
当
时，函数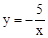
的图象在【 】
| A．第四象限 | B．第三象限 | C．第二象限 | D．第一象限 |
如图，点P（﹣3，2）是反比例函数
（k≠0）的图象上一点，则反比例函数的解析式【 】
A． | B． | C． | D． |
若点A（1，y1）、B（2，y2）都在反比例函数
的图象上，则y1、y2的大小关系为
| A．y1＜y2 | B．y1≤y2 | C．y1＞y2 | D．y1≥y2 |