题目内容
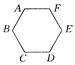
【题目】如图所示,已知六边形ABCDEF中,∠A=∠B=∠C=∠D=∠E=∠F=120°.试说明AB+BC=EF+ED.
【答案】见解析
【解析】分析:分别延长AB、DC相交于点M,延长AF、DE相交于点N,通过作辅助线我们可以得到∠MBC=∠MCB=60°,再结合三角形内角和定理即可判断△BMC是等边三角形,同理还可以得出△EFN是等边三角形;由“两组对角分别相等的四边形是平行四边形”可知四边形AMDN是平行四边形,从而可以得到AM=DN即可得出结果.
本题解析:分别延长AB、DC相交于点M,延长AF、DE相交于点N.
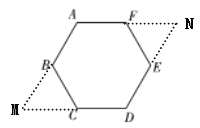
∵∠ABC=∠DCB=120°,
∴∠MBC=∠MCB=60°.
∵在△MBC中,∠MBC=∠MCB=60°,
∴∠CMB=60°.
同理∠FNE=60°.
∵∠MBC=∠MCB=60°,∠CMB=60°,
∴△BMC是等边三角形.
同理△EFN是等边三角形.
∵∠BAN=∠CDE=120°,∠CMB=60°,∠FNE=60°,
∴四边形AMDN是平行四边形,
∴AM=DN.
∵△BMC、△EFN是等边三角形,
∴BC=BM,EF=EN.
∵AM=DN,BC=BM,EF=EN,
∴AB+BC=DE+EF.

练习册系列答案
相关题目