Question

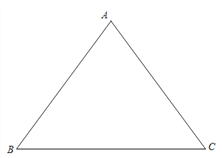
【题目】如图，已知在中， ， .

(1)求的长；

(2)点D在边AB上，且AD=1， 为边上一动点，连接DM．当是直角三角形时，求BM的长．

Answer 1

【答案】（1）的长是12；（2）BM的长是5.4．

【解析】试题分析：（1）作AH⊥BC于D，如图1，根据等腰三角形的性质得BH=CH，在Rt△ABH中利用正切的定义的tan∠B= ，设AH=4a，BH=3a，由勾股定理得到AB=5a，则5a=10，解得a=2，所以BC=2BH=12；（2）当时，设DM=4x，则BM=3x,由BM2+DM2=BD2,求得BM的长；当时，由tan∠B=求得DM＝15，不符合题意舍去，所以BM＝5.4；

试题解析：

(1) 作AH⊥BC于D，如图所示：

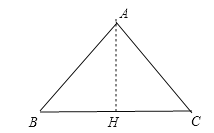
∵AB=AC=10
∴BH=CH，
在Rt△ABH中，tan∠B=，

设AH=4a，BH=3a，
∴AB=

∴5a=10，解得a=2，
∴BC=2BH=12；

(2)若，如图所示：

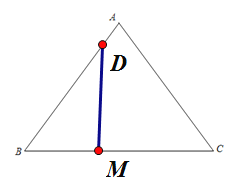
∵AD=1,AB=10,

∴BD=9,

设DM=4x，则BM=3x,由BM2+DM2=BD2,得x= 或x= （舍去）

∴BM=5.4;

若，如图所示：

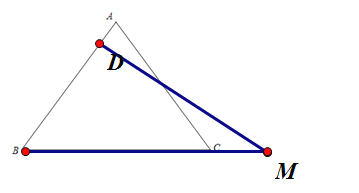
∵AD=1,AB=10,

∴BD=9,

∵tan∠B=，

∴BM=15，

因为15>12，所以BM=15应舍去；

所以当是直角三角形时，求BM的长为5.4。