��Ŀ����
����Ŀ����ͼ��������y=��x2+bx+c�Ķ���ΪQ����������x�ύ��A����1��0����B��5��0�����㣬��y�ύ�ڵ�C��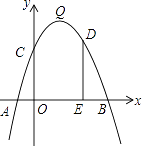
��1���������ߵĽ���ʽ���䶥��Q�����ꣻ
��2���ڸ�����������һ��P��ʹ��S��PAB=S��ABC �� �����P�����꣺
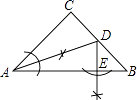
��3������D�ǵ�һ�����������ϵ�һ�����㣬����D��DE��x�ᣬ����ΪE����һ��ͬѧ˵�����ڵ�һ�����������ϵ����е��У������ߵĶ���Q��x�������Զ�����Ե���D�˶�����Qʱ������D��E��O�ij�����������ͬѧ��˵����ȷ����˵�����ɣ�
���𰸡�
��1��
�⣺��������y=��x2+bx+c��x�ύ��A����1��0����B��5��0�����㣬
��y=����x+1����x��5��=��x2+4x+5��
�������ߵĽ���Ϊy=��x2+4x+5��
��y=��x2+4x+5=����x��2��2+9��
�ඥ��Q������Ϊ��2��9��
��2��
�⣺��y=��x2+4x+5�У���x=0ʱ��y=5��
���C����������0��5����
���P��������Ϊa��
��S��PAB=S��ABC����|a|=5��
���a=��5��
��a=5ʱ����x2+4x+5=5�����x=0����ȥ����x=4����ʱ��p������Ϊ��4��5����
��a=��5ʱ����x2+4x+5=��5�����x=2�� ![]() ����ʱ��p������Ϊ��2+
����ʱ��p������Ϊ��2+ ![]() ����5����2��
����5����2�� ![]() ����5����
����5����
���ϣ���p������Ϊ��4��5����2+ ![]() ����5����2��
����5����2�� ![]() ����5��
����5��
��3��
�⣺���ͬѧ��˵������ȷ
���ɣ���D��t����t2+4t+5��������D��E��O�ij���ΪL��
��L=��t2+4t+5+t=����t�� ![]() ��2+
��2+ ![]() ��
��
��a��0��
�൱t= ![]() ʱ��L���ֵ=
ʱ��L���ֵ= ![]() ��
��
������D���Q�غ�ʱ��L=9+2=11�� ![]() ��
��
���ͬѧ��˵������ȷ
����������1����������y=��x2+bx+c��x�ύ��A����1��0����B��5��0�����㣬��ֱ�����ý���ʽ���y=����x+1����x��5��=��x2+4x+5���̶���ö���Q�����ꣻ��2���������P��������Ϊa����S��PAB=S��ABC �� �ɵ�a=��5��Ȼ��ɵé�x2+4x+5=��5���̶���õ�P�����ꣻ��3��������D��t����t2+4t+5��������D��E��O�ij���ΪL����ɵ�L=��t2+4t+5+t��Ȼ��������ֵ������֪���ͬѧ���Ƿ�˵����ȷ��

 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�����Ŀ�����������ҹ��ܶ����������������������ij�м���Ϊ���˽⡰������������Ҫ������������˸��в��������Ե��������������������������в�������ͳ��ͼ����

��� | �۵� | Ƶ���������� |
A | ������ѹ�ͣ����������� | m |
B | ����ҳ�����ʪ�ȵ� | 40 |
C | ����β���ŷ� | n |
D | ������ɵ���Ⱦ | 120 |
E | ���� | 60 |
�����ͼ�����ṩ����Ϣ����������⣺
��1����գ�m�� ��n�� ������ͳ��ͼ��E����ռ�İٷֱ�Ϊ % ��
��2���������˿�Լ��400���ˣ�����������г�D�顰�۵㡱������������
��3�����ڡ�����������������⣬���ü�̵����Է������飮