题目内容
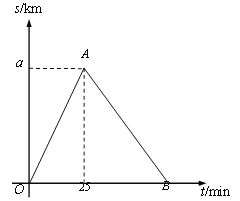
【题目】某市举行“迷你马拉松”长跑比赛，运动员从起点甲地出发，跑到乙地后，沿原路线再跑回点甲地．设该运动员离开起点甲地的路程s(km)与跑步时间t(min)之间的函数关系如图所示．已知该运动员从甲地跑到乙地时的平均速度是0.2 km/min，根据图像提供的信息，解答下列问题：
（1）a＝ km；
（2）组委会在距离起点甲地3km处设立一个拍摄点P，该运动员从第一次过P点到第二次过P点所用的时间为24min．
①求AB所在直线的函数表达式；
②该运动员跑完全程用时多少min？
【答案】（1）5千米．（2）直线AB 解析式为s＝－
t＋
．60分.
【解析】（1）∵从甲地跑到乙地时的平均速度是0.2 km/min，用时25分钟，
∴a＝0.2×25＝5千米．…………2分
（2）①∵线段OA经过点
O（0，0），A（25，5），
∴线段OA函数表达式为s＝0.2t（0≤t≤25），……3分
∴当s＝3时， 由0.2t＝3，解得t＝15，
∵该运动员从第一次过P点到第二次过P点所用的时间为24min．
∴该运动员从起点点到第二次经过C点所用的时间是15＋24＝39 min，………4分
∴直线AB经过（25，5），（39，3），设直线AB解析式s＝kt＋b，
则5＝25k＋b，3＝39k＋b，∴解得，k＝－
，b＝
∴直线AB 解析式为s＝－t＋．………………6分
②该运动员跑完赛程用的时间即为直线AB与x轴交点的横坐标，
∴当s＝0时，－ t＋＝0，解得t＝60．
∴该运动员跑完赛程用时60分钟．
【题目】人民商场销售某种冰箱，每台进价为2500元，市场调研表明：当每台销售价定为2900元时，平均每天能售出8台；每台售价每降低50元，平均每天能多售出4台．设该种冰箱每台的销售价降低了x元．
（1）填表：
每天售出的冰箱台数（台） | 每台冰箱的利润（元） | |
降价前 | 8 | |
降价后 |
（2）若商场要想使这种冰箱的销售利润平均每天达到5000元，则每台冰箱的售价应定为多少元？
