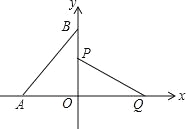
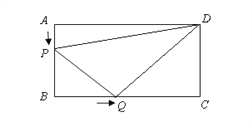
ĢāÄæÄŚČŻ
”¾ĢāÄæ”æŌĶĮĄķ½ā£ŗ
ČōA”¢B”¢CĪŖŹżÖįÉĻČżµć£¬ČōµćCµ½AµÄ¾ąĄėŹĒµćCµ½BµÄ¾ąĄė2±¶£¬ĪŅĆĒ¾Ķ³ĘµćCŹĒ”¾A£¬B”æµÄŗĆµć£®
ČēĶ¼1£¬µćA±ķŹ¾µÄŹżĪŖ©1£¬µćB±ķŹ¾µÄŹżĪŖ2£®±ķŹ¾1µÄµćCµ½µćAµÄ¾ąĄėŹĒ2£¬µ½µćBµÄ¾ąĄėŹĒ1£¬ÄĒĆ“µćCŹĒ”¾A£¬B”æµÄŗĆµć£®
ÖŖŹ¶ŌĖÓĆ£ŗ
£Ø1£©ČēĶ¼1£¬±ķŹ¾0µÄµćDµ½µćAµÄ¾ąĄėŹĒ1£¬µ½µćBµÄ¾ąĄėŹĒ2£¬ÄĒĆ“µćD ”¾A£¬B”æµÄŗĆµć£»£ØĒėŌŚŗįĻßÉĻĢīŹĒ»ņ²»ŹĒ£©
£Ø2£©ČēĶ¼2£¬M”¢NĪŖŹżÖįÉĻĮ½µć£¬µćMĖł±ķŹ¾µÄŹżĪŖ4£¬µćNĖł±ķŹ¾µÄŹżĪŖ©2£®Źż Ėł¶ŌÓ¦µÄµćŹĒ”¾M£¬N”æµÄŗƵć£ØŠ“³öĖłÓŠæÉÄܵÄĒéæö£©£»
ĶŲÕ¹ĢįÉż£ŗ
£Ø3£©ČēĶ¼3£¬A”¢BĪŖŹżÖįÉĻĮ½µć£¬µćAĖł±ķŹ¾µÄŹżĪŖ©20£¬µćBĖł±ķŹ¾µÄŹżĪŖ40£®ĻÖÓŠŅ»Ö»µē×ÓĀģŅĻP“ÓµćB³ö·¢£¬ŅŌ4øöµ„Ī»ĆæĆėµÄĖŁ¶ČĻņ×óŌĖ¶Æ£¬µ½“ļµćAĶ£Ö¹£®µ±¾¹ż¼øĆėŹ±£¬P”¢AŗĶBÖŠĒ”ÓŠŅ»øöµćĪŖĘäÓąĮ½µćµÄŗƵć£æ£ØŠ“³öĖłÓŠĒéæö£©
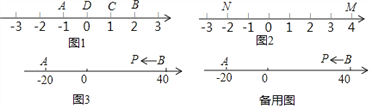
”¾“š°ø”æ£Ø1£©²»ŹĒ£»£Ø2£©0»ņ-8£»£Ø3£©5£¬10£¬7.5.
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©øł¾Ż¶ØŅå·¢ĻÖ£ŗŗƵć±ķŹ¾µÄŹżµ½”¾A£¬B”æÖŠ£¬Ē°ĆęµÄµćAŹĒµ½ŗóĆęµÄŹżBµÄ¾ąĄėµÄ2±¶£¬“Ó¶ųµĆ³ö½įĀŪ£»
£Ø2£©µćMµ½µćNµÄ¾ąĄėĪŖ6£¬·ÖČżµČ·ÖĪŖ·ŻĪŖ2£¬øł¾Ż¶ØŅåµĆ£ŗŗƵćĖł±ķŹ¾µÄŹżĪŖ0»ņ-8£»
£Ø3£©øł¾ŻŗƵćµÄ¶ØŅåæÉÖŖ·ÖĮ½ÖÖĒéæö£ŗ¢ŁPĪŖ£ØA£¬B£©µÄŗĆµć£»¢ŚPĪŖ£ØB£¬A£©µÄŗĆµć£»¢ŪBĪŖ£ØA£¬P£©µÄŗĆµć£®ÉčµćP±ķŹ¾µÄŹżĪŖx£¬øł¾ŻŗƵćµÄ¶ØŅåĮŠ³ö·½³Ģ£¬½ų¶ųµĆ³ötµÄÖµ£®
ŹŌĢā½āĪö£ŗ£Ø1£©ČēĶ¼1£¬”ßµćDµ½µćAµÄ¾ąĄėŹĒ1£¬µ½µćBµÄ¾ąĄėŹĒ2£¬
øł¾ŻŗƵćµÄ¶ØŅåµĆ£ŗDB=2DA£¬
ÄĒĆ“µćD²»ŹĒ”¾A£¬B”æµÄŗƵć
£Ø2£©ČēĶ¼2£¬4-£Ø-2£©=6£¬6”Ā3”Į2=4£¬
¼“¾ąĄėµćM4øöµ„Ī»£¬¾ąĄėµćN2øöµ„Ī»µÄµć¾ĶŹĒĖłĒóµÄŗƵć0£»
”ąŹż0Ėł±ķŹ¾µÄµćŹĒ”¾M£¬N”æµÄŗĆµć£»
4-£Ø-8£©=12£¬-2-£Ø-8£©=6£¬
Ķ¬Ąķ£ŗŹż-8Ėł±ķŹ¾µÄµćŅ²ŹĒ”¾M£¬N”æµÄŗĆµć£»
”ąŹż0»ņ-8Ėł±ķŹ¾µÄµćŹĒ”¾M£¬N”æµÄŗĆµć£»
£Ø3£©ÉčµćP±ķŹ¾µÄŹżĪŖx£¬ŌņPA=x+20£¬PB=40-x£¬AB=40-£Ø-20£©=60£¬
·ÖČżÖÖĒéæö£ŗ
¢ŁPĪŖ£ØA£¬B£©µÄŗĆµć£®
ÓÉĢāŅā£¬µĆPA=2PB£¬¼“x-£Ø-20£©=2£Ø40-x£©£¬
½āµĆx=20£¬
”ąt=£Ø40-20£©”Ā4=5£ØĆė£©£»
¢ŚPĪŖ£ØB£¬A£©µÄŗĆµć£®
ÓÉĢāŅā£¬µĆPB=2PA£¬¼“40-x=2£Øx+20£©£¬
½āµĆx=0£¬
”ąt=£Ø40-0£©”Ā4=10£ØĆė£©£»
¢ŪBĪŖ£ØA£¬P£©µÄŗĆµć£®
ÓÉĢāŅā£¬µĆAB=2PA£¬¼“60=2£Øx+20£©
½āµĆx=10£¬
“ĖŹ±£¬µćPĪŖABµÄÖŠµć£¬¼“AŅ²ĪŖ£ØB£¬P£©µÄŗĆµć£¬
”ąt=30”Ā4=7.5£ØĆė£©£»
×ŪÉĻæÉÖŖ£¬µ±tĪŖ5Ćė”¢10Ćė»ņ7.5ĆėŹ±£¬P”¢AŗĶBÖŠĒ”ÓŠŅ»øöµćĪŖĘäÓąĮ½µćµÄŗĆµć£®

”¾ĢāÄæ”æ(2016ɽ¶«Ź”ĮijĒŹŠµŚ21Ģā)ĪŖĮĖČĆŹé¼®æŖĶŲѧɜµÄŹÓŅ°£¬ĢÕŅ±Ń§ÉśµÄĒé²Ł£¬ĻņŃō֊ѧæŖÕ¹ĮĖ”°ĪåøöŅ»”±æĪĶāŌĶĮ»ī¶Æ£¬ĪŖĮĖ½āČ«Š£Ń§ÉśæĪĶāŌĶĮĒéæö£¬³éŃłµ÷²éĮĖ50ĆūŃ§ÉśĘ½¾łĆæĢģæĪĶāŌĶĮŹ±¼ä£Øµ„Ī»£ŗmin£©£¬½«³é²éµĆµ½µÄŹż¾Ż·Ö³É5×飬ĻĀĆęŹĒÉŠĪ“Ķź³ÉµÄʵŹż”¢ĘµĀŹ·Ö²¼±ķ£ŗ
×鱚 | ·Ö×é | ʵŹż£ØČĖŹż£© | ʵĀŹ |
1 | 10”Üt£¼30 | 0.16 | |
2 | 30”Üt£¼50 | 20 | |
3 | 50”Üt£¼70 | 0.28 | |
4 | 70”Üt£¼90 | 6 | |
5 | 90”Üt£¼110 |
£Ø1£©½«±ķÖŠæÕøń“¦µÄŹż¾Ż²¹Č«£¬Ķź³ÉÉĻĆęµÄʵŹż”¢ĘµĀŹ·Ö²¼±ķ£»
£Ø2£©ĒėŌŚøų³öµÄĘ½ĆęÖ±½Ē×ų±źĻµÖŠ»³öĻąÓ¦µÄʵŹżÖ±·½Ķ¼£»
£Ø3£©Čē¹ūøĆŠ£ÓŠ1500Ćūѧɜ£¬ĒėÄć¹Ą¼ĘøĆŠ£¹²ÓŠ¶ąÉŁĆūŃ§ÉśĘ½¾łĆæĢģŌĶĮŹ±¼ä²»ÉŁÓŚ50min£æ