题目内容
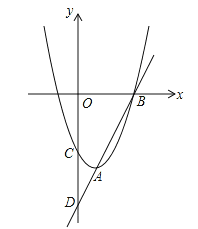
【题目】如图,抛物线C1是二次函数y=x2﹣10x在第四象限的一段图象,它与x轴的交点是O、A1;将C1绕点A1旋转180°后得抛物线C2;交x轴于点A2;再将抛物线C2绕A2点旋转180°后得抛物线C3,交x轴于点A3;如此反复进行下去…
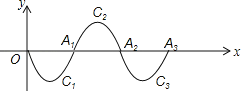
(1)抛物线C3与x轴的交点A3的坐标是多少?抛物线Cn与x轴的交点An的坐标是多少?
(2)若某段抛物线上有一点P(2016,a),试求a的值.
【答案】(1)A3的坐标为(30,0),抛物线Cn与x轴的交点An的坐标为(10n,0);(2)24.
【解析】
试题分析:(1)通过解方程x2﹣10x=0可得到A1(10,0),则OA1=10,再利用旋转的性质得OA2=2OA1=20,OA3=3OA1=30,…,OAn=nOA1=10n,所以A3的坐标为(30,0),An的坐标为(10n,0);
(2)由于2016=201×10+16,则可判断点P(2016,a)在抛物线C202上,利用(1)中的结论得到抛物线C202与x轴的交点坐标为(2010,0),(2020,0),抛物线开口向下,利用交点式写出抛物线C202的解析式为y=﹣(x﹣2010)(x﹣2020),然后计算自变量为2016所对应的函数值即可.
解:(1)当y=0时,x2﹣10x=0,解得x1=0,x2=10,则A1(10,0),OA1=10,
因为OA2=2OA1=20,OA3=3OA1=30,同理可得OAn=nOA1=10n,
所以A3的坐标为(30,0),抛物线Cn与x轴的交点An的坐标为(10n,0);
(2)因为2016=201×10+16,
所以点P(2016,a)在抛物线C202上,
而抛物线C202与x轴的交点坐标为(2010,0),(2020,0),抛物线开口向下,
所以抛物线C202的解析式为y=﹣(x﹣2010)(x﹣2020),
把点P(2016,a)代入得a=﹣6×(﹣4)=24,
即a的值为24.