题目内容
【题目】在△ABC中,点D,E,F分别在AB,BC,AC上,且∠ADF+∠DEC=180°,∠AFE=∠BDE.
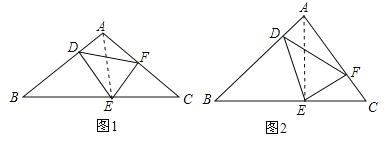
(1)如图1,当DE=DF时,图1中是否存在与AB相等的线段?若存在,请找出,并加以证明;若不存在,说明理由;
(2)如图2,当DE=kDF(其中0<k<1)时,若∠A=90°,AF=m,求BD的长(用含k,m的式子表示).

【答案】(1)AB=BE;(2)BD=![]() .
.
【解析】
试题分析:(1)如图1,连结AE.由DE=DF,得到∠DEF=∠DFE,由∠ADF+∠DEC=180°,得到∠ADF=∠DEB.由∠AFE=∠BDE,得到∠AFE+∠ADE=180°,得到A、D、E、F四点共圆,由圆周角定理得出∠DAE=∠DFE=∠DEF,∠ADF=∠AEF.再由∠ADF=∠DEB=∠AEF,得出∠AEF+∠AED=∠DEB+∠AED,则∠AEB=∠DEF=∠BAE,由等角对等边得出AB=BE;
(2)如图2,连结AE.由A、D、E、F四点共圆,得到∠ADF=∠AEF,由∠DAF=90°,得到∠DEF=90°,再证明∠DEB=∠AEF.又∠AFE=∠BDE,得到△BDE∽△AFE,利用相似三角形对应边成比例得到![]() .在Rt△DEF中,利用勾股定理求出EF=
.在Rt△DEF中,利用勾股定理求出EF=![]() DF,然后将AF=m,DE=kDF代入,计算即可求解.
DF,然后将AF=m,DE=kDF代入,计算即可求解.
试题解析:(1)如图1,连结AE.∵DE=DF,∴∠DEF=∠DFE,∵∠ADF+∠DEC=180°,∴∠ADF=∠DEB,∵∠AFE=∠BDE,∴∠AFE+∠ADE=180°,∴A、D、E、F四点共圆,∴∠DAE=∠DFE=∠DEF,∠ADF=∠AEF,∵∠ADF=∠DEB=∠AEF,∴∠AEF+∠AED=∠DEB+∠AED,∴∠AEB=∠DEF=∠BAE,∴AB=BE;
(2)如图2,连结AE.∵∠AFE=∠BDE,∴∠AFE+∠ADE=180°,∴A、D、E、F四点共圆,∴∠ADF=∠AEF,∵∠DAF=90°,∴∠DEF=90°,∵∠ADF+∠DEC=180°,∴∠ADF=∠DEB,∵∠ADF=∠AEF,∴∠DEB=∠AEF,在△BDE与△AFE中,∵∠DEB=∠AEF,∠BDE=∠AFE,∴△BDE∽△AFE,∴![]() ,在直角△DEF中,∵∠DEF=90°,DE=kDF,∴EF=
,在直角△DEF中,∵∠DEF=90°,DE=kDF,∴EF=![]() =
=![]() DF,∴
DF,∴![]() =
=![]() ,∴BD=
,∴BD=![]() .
.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案