��Ŀ����
����Ŀ����ͼ������QPN�Ķ���P��������ABCD�����Խ��ߵĽ��㴦����QPN=��������QPN�Ƶ�P��ת����ת��������QPN�����߷ֱ���������ABCD�ı�AD��CD���ڵ�E�͵�F����F���C��D���غϣ���
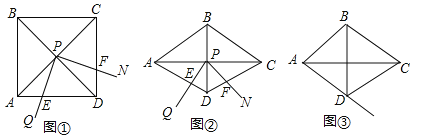
��1����ͼ�٣�����=90��ʱ��DE��DF��AD֮�������������ϵ�� ��
��2����ͼ�ڣ���ͼ���е�������ABCD��Ϊ��ADC=120������Σ������������䣬����=60��ʱ����1���еĽ��۱�ΪDE+DF=![]() AD�������֤����
AD�������֤����
��3���ڣ�2���������£�����ת��������QPN�ı�PQ������AD���ڵ�E�������������䣬̽���������˶��仯�����У�DE��DF��AD֮�������������ϵ��ֱ��д�����ۣ����ü���֤����
���𰸡���1��DE+DF=AD����2��֤���������������3���ٵ���E����AD��ʱ��DE+DF=![]() AD���ڵ���E����AD���ӳ�����ʱ��DF��DE =
AD���ڵ���E����AD���ӳ�����ʱ��DF��DE =![]() AD��
AD��
��������
�����������1��֤����APE�ա�DPF���õ�AE=DF�����ɵó�����DE+DF=AD��
��2��ȡAD���е�M������PM����֤����MDP�ǵȱ������Σ���MPE�ա�FPD������ME=DF����DE+ME=![]() AD�����ɵó�DE+DF=
AD�����ɵó�DE+DF=![]() AD��
AD��
��3���ٵ���E����AD��ʱ��DE+DF=![]() AD���ڵ���E����AD���ӳ�����ʱ��DF��DE =
AD���ڵ���E����AD���ӳ�����ʱ��DF��DE =![]() AD��
AD��
�����������1��������ABCD�ĶԽ���AC��BD���ڵ�P����PA=PD����PAE=��PDF=45�㣬�ߡ�APE+��EPD=��DPF+��EPD=90�㣬���APE=��DPF������APE����DPF�����ߡ�APE=��DPF��PA=PD����PAE=��PDF�����APE�ա�DPF��ASA������AE=DF����DE+DF=AD��
��2����ͼ�ڣ�ȡAD���е�M������PM�����ı���ABCDΪ��ADC=120������Σ���BD=AD����DAP=30�㣬��ADP=��CDP=60�㣬���MDP�ǵȱ������Σ���PM=PD����PME=��PDF=60�㣬�ߡ�PAM=30�㣬���MPD=60�㣬�ߡ�QPN=60�㣬���MPE=��FPD������MPE����FPD�У��ߡ�PME=��PDF��PM=PD����MPE=��FPD�����MPE�ա�FPD��ASA������ME=DF����DE+DF=![]() AD��
AD��

��3����ͼ���������˶��仯�����У��ٵ���E����AD��ʱ��DE+DF=![]() AD��
AD��
�ڵ���E����AD���ӳ�����ʱ��DF��DE =![]() AD��
AD��
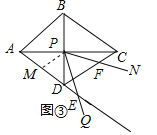
����ͼ3��ȡAD�е�M������PM��֤����MPE�ա�DPF��




