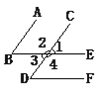题目内容
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.
(1)判断四边形ACGD的形状,并说明理由.
(2)求证:BE=CD,BE⊥CD.

【答案】(1)四边形ACGD为平行四边形,理由见解析;(2)证明见解析.
【解析】
(1)利用等腰直角三角形的性质易得BD=2BC,因为G为BD的中点,可得BG=BC,由∠CGB=45°,∠ADB=45°得AD∥CG,由∠CBD+∠ACB=180°,得AC∥BD,得出四边形ACGD为平行四边形;
(2)利用全等三角形的判定证得△DAC≌△BAE,由全等三角形的性质得BE=CD;首先证得四边形ABCE为平行四边形,再利用全等三角形的判定定理得△BCE≌△CAD,易得∠CBE=∠ACD,由∠ACB=90°,易得∠CFB=90°,得出结论.
(1)解:∵△ABC是等腰直角三角形,∠ACB=90°,
∴AB=![]() BC,
BC,
∵△ABD和△ACE均为等腰直角三角形,
∴BD=![]() =
=![]() =2BC,
=2BC,
∵G为BD的中点,
∴BG=![]() BD=BC,
BD=BC,
∴△CBG为等腰直角三角形,
∴∠CGB=45°,
∵∠ADB=45°,
AD∥CG,
∵∠ABD=45°,∠ABC=45°
∴∠CBD=90°,
∵∠ACB=90°,
∴∠CBD+∠ACB=180°,
∴AC∥BD,
∴四边形ACGD为平行四边形;
(2)证明:∵∠EAB=∠EAC+∠CAB=90°+45°=135°,
∠CAD=∠DAB+∠BAC=90°+45°=135°,
∴∠EAB=∠CAD,
在△DAC与△BAE中,
 ,
,
∴△DAC≌△BAE,
∴BE=CD;
∵∠EAC=∠BCA=90°,EA=AC=BC,
∴四边形ABCE为平行四边形,
∴CE=AB=AD,
在△BCE与△CAD中,
 ,
,
∴△BCE≌△CAD,
∴∠CBE=∠ACD,
∵∠ACD+∠BCD=90°,
∴∠CBE+∠BCD=90°,
∴∠CFB=90°,
即BE⊥CD.

 天天练口算系列答案
天天练口算系列答案