题目内容
【题目】如图,线段AC、BD交于点M,过B、D两点分别作AC的垂线段BF、DE,AB=CD.
(1)若∠A=∠C,求证FM=EM;
(2)若FM=EM,则∠A=∠C.是真命题吗?(直接判断,不必证明)

【答案】(1)证明见解析;(2)真命题,理由见解析.
【解析】试题分析:(1)由条件可先证明△ABF≌△CDE,可得BF=DE,再证明△BFM≌△DEM,可得到FM=EM;
(2)由条件可先证明△BFM≌△DEM,可得BF=DE,再证明△ABF≌△CDE,可得∠A=∠C.
试题解析:(1)∵BF⊥AC,DE⊥AC,
∴∠AFB=∠CED,
在△ABF和△CDE中, 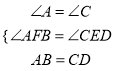 ,
,
∴△ABF≌△CDE(AAS),
∴BF=DE,
在△BFM和△DEM中, 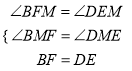 ,
,
∴△BFM≌△DEM(AAS),
∴FM=EM;
(2)真命题;理由如下:
∵BF⊥AC,DE⊥AC,
∴∠BFM=∠DEM=90°,
在△BFM和△DEM中, 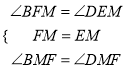 ,
,
∴△BFM≌△DEM(ASA),
∴BF=DE,
在Rt△ABF和Rt△CDE中, ![]()
∴Rt△ABF≌Rt△CDE(HL),
∴∠A=∠C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目