��Ŀ����
����Ŀ����ͼ��������y=��x2+bx+c����A����1��0����B��3��0�����㣬����y�ύ�ڵ�C����D�������ߵĶ��㣬�����ߵĶԳ���DE��x���ڵ�E������BD��

��1����A��B��C����������ߵĺ�������ʽ��
��2����P���߶�BD��һ�㣬��PE=PCʱ�����P�����ꣻ
��3���ڣ�2���������£�����P��PF��x���ڵ�F��GΪ��������һ���㣬MΪx����һ���㣬NΪֱ��PF��һ���㣬����F��M��GΪ������ı�����������ʱ���������M�����꣮
���𰸡���1��y=��x2+2x+3����2����2��2������3����![]() ��0������
��0������![]() ��0������
��0������![]() ��0������
��0������![]() ��0����
��0����
��������
�����������1�����ô���ϵ���������A��B��C����������ߵĺ�������ʽ����2������PC��PE�����ù�ʽ�������D�����꣬���ô���ϵ�������ֱ��BD�Ľ���ʽ�������P������Ϊ��x����2x+6�������ù��ɶ�����ʾ��PC2��PE2�����������г����̣��ⷽ�����x��ֵ�����������P�����ꣻ��3�����M������Ϊ��a��0������ʾ����G�����꣬���������ε������г����̣��ⷽ�̼��ɣ�
�����������1����������y=��x2+bx+c����A����1��0����B��3��0�����㣬
��![]() �� ��ã�
�� ��ã�![]() �� ������A��B��C����������ߵĺ�������ʽΪy=��x2+2x+3��
�� ������A��B��C����������ߵĺ�������ʽΪy=��x2+2x+3��
��2����ͼ1������PC��PE�� x=��![]() =��
=��![]() =1�� ��x=1ʱ��y=4��
=1�� ��x=1ʱ��y=4��
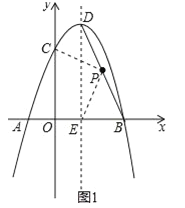
����D������Ϊ��1��4���� ��ֱ��BD�Ľ���ʽΪ��y=mx+n����![]() �� ��ã�
�� ��ã�![]() ��
��
��ֱ��BD�Ľ���ʽΪy=��2x+6�� ���P������Ϊ��x����2x+6����
��PC2=x2+��3+2x��6��2��PE2=��x��1��2+����2x+6��2�� ��PC=PE��
��x2+��3+2x��6��2=��x��1��2+����2x+6��2�� ��ã�x=2�� ��y=��2��2+6=2�� ����P������Ϊ��2��2����
��3�����M��������a��0�������G��������a����a2+2a+3����
����F��M��GΪ������ı����������Σ� ��FM=MG����|2��a|=|��a2+2a+3|��
��2��a=��a2+2a+3ʱ�� �����ã�a2��3a��1=0�� ��ã�a=![]() ��
��
��2��a=������a2+2a+3��ʱ�� �����ã�a2��a��5=0�� ��ã�a=![]() ��
��
������F��M��GΪ������ı�����������ʱ����M������Ϊ��![]() ��0������
��0������![]() ��0������
��0������![]() ��0������
��0������![]() ��0����
��0����

 ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�




