题目内容
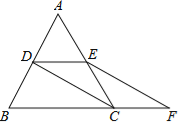
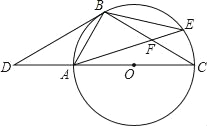
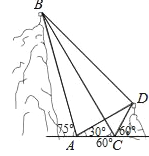
【题目】如图,B,D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°,30°.于水面C处测得B点和D点的仰角均为60°,AC=0.1km.
(1)试探究图中B,D间距离与另外哪两点间距离相等;
(2)求B点距水平面的高度(计算结果精确到0.01km,参考数据:![]() ≈1.73,tan75°≈3.73)
≈1.73,tan75°≈3.73)
【答案】(1)BD=BA (2)0.32km
【解析】
(1)由已知条件易得∠AOC=90°,由此可得BC⊥AD,由∠DCF=∠DAC+∠ADC=60°结合∠DAC=30°可得∠ADC=30°,由此可得AC=DC,从而说明BC是AD的垂直平分线,由此即可得到BD=BA;
(2)过点B作BE⊥AC于点E,设AE=x,则由已知条件易得:BE=AE·tan∠BAE=tan75°·x,BE=CE·tan∠BCE=(0.1+x)tan30°,由此即可得到关于x的方程,解方程即可求得AE的长,进而可得BE的长.
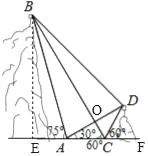
(1)如图,
在△ACD中,∵∠DAC=30°,∠ACB=∠DCF=60°,
∴∠AOC=180°﹣∠DAC﹣∠ACB=90°,∠ADC=∠DCF﹣∠DAC=30°,
∴AC=DC、BC⊥AD,
∴BC是AD的中垂线,
∴BD=BA;
(2)如下图,作BE⊥AC,交CA延长线于点E,
设AE=x,
则BE=AEtan∠BAE=tan75°x,
∵AC=0.1,
∴CE=AC+AE=0.1+x,
在Rt△BCE中,∵tan∠BCE=![]() ,
,
∴tan60°=![]() ,即
,即![]() ,
,
解得:x=0.0865,
则BE=tan75°x=3.73×0.0865≈0.32,
答:B点距水平面的高度约为0.32km.

 智慧小复习系列答案
智慧小复习系列答案【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,其中的20m3仍按2元/m3计算,超过部分按2.6元/m3计算.设某户家庭月用水量xm3.
月份 | 4月 | 5月 | 6月 |
用水量 | 15 | 17 | 21 |
(1)用含x的式子表示:
当0≤x≤20时,水费为 元;
当x>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?