题目内容
【题目】(1)特例探究.
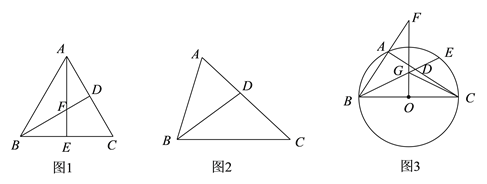
如图(1),在等边三角形ABC中,BD是∠ABC的平分线,AE是BC边上的高线,BD和AE相交于点F.
请你探究![]() 是否成立,请说明理由;请你探究
是否成立,请说明理由;请你探究![]() 是否成立,并说明理由.
是否成立,并说明理由.
(2)归纳证明.
如图(2),若△ABC为任意三角形,BD是三角形的一条内角平分线,请问![]() 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
(3)拓展应用.
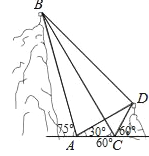
如图(3),BC是△ABC外接圆⊙O的直径,BD是∠ABC的平分线,交⊙O于点E,过点O作BC的垂线,交BA的延长线于点F,交BD于点G,连接CG,其中cos∠ACB=![]() ,请直接写出
,请直接写出![]() 的值;若△BGF的面积为S,请求出△COG的面积(用含S的代数式表示).
的值;若△BGF的面积为S,请求出△COG的面积(用含S的代数式表示).
【答案】(1)成立,证明见解析;(2)成立,证明见解析;(3)![]() S.
S.
【解析】
(1)由等边三角形的性质结合已知条件易得:AD=CD,AB=BC,∠AEB=90°,∠BAF=∠ABF=∠CBF=30°,由此可得AF=BF=2EF,从而可得![]() ,
,![]() ;
;
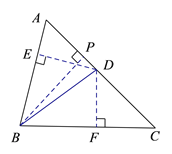
(2)如下图,过点D作DE⊥AB于点E,DF⊥BC于点F,过点B作BP⊥AC于点P,则易得DE=DF,由此可得S△ABD=![]() AB·DE=
AB·DE=![]() AD·BP,S△CBD=
AD·BP,S△CBD=![]() BC·DF=
BC·DF=![]() CD·BP,把两个等式相比即可得到所求结论了;
CD·BP,把两个等式相比即可得到所求结论了;
(3)①由BC是⊙O的直径可得∠BAC=90°,结合cos∠ACB=![]() 可得sin∠ACB=
可得sin∠ACB=![]() ,再由(2)中结论即可得到
,再由(2)中结论即可得到![]() ;②由已知条件易得
;②由已知条件易得![]() ,由OF⊥BC可得
,由OF⊥BC可得![]() ,从而可得
,从而可得![]() ,由此即可得到S△COG=
,由此即可得到S△COG=![]() .
.
(1)![]() ,
,![]() ,理由如下:
,理由如下:
∵△ABC为等边三角形,BD是∠ABC的平分线,AE是BC边上的高线,
∴AD=CD=![]() AC,BE=
AC,BE=![]() BC ,AB=BC,∠AEB=90°,∠BAF=∠ABF=∠CBF=30°,
BC ,AB=BC,∠AEB=90°,∠BAF=∠ABF=∠CBF=30°,
∴AF=BF=2EF,
∴![]() ,
,![]() ;
;
(2)![]() 一定成立,理由如下:
一定成立,理由如下:
如下图,过点D作DE⊥AB于点E,DF⊥BC于点F,过点B作BP⊥AC于点P,
∵BD是∠ABC的平分线,
∴DE=DF,
∵S△ABD=![]() AB·DE=
AB·DE=![]() AD·BP,S△CBD=
AD·BP,S△CBD=![]() BC·DF=
BC·DF=![]() CD·BP,
CD·BP,
∴![]()
∴![]() .
.
(3)∵BC为直径,
∴∠BAC=90°.
在Rt△ABC中,∠BAC=90°,cos∠ACB=![]() ,
,
∴sin∠ACB=![]() .
.
∵BD是∠ABC的平分线,
∴![]() .
.
∵点G在∠ABC的平分线上,
∴△BGF和△COG等高(分别以BF、CO为底),
∴![]() .
.
∵FO⊥BC,
∴![]() =cos∠ABC=sin∠ACB=
=cos∠ABC=sin∠ACB=![]() ,
,
又∵S△BGF=S,
∴![]() ,
,
∴S△COG=![]() S.
S.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案