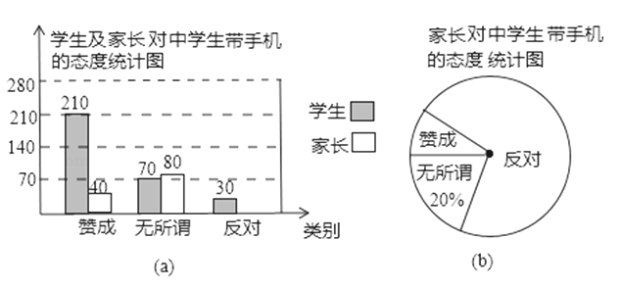
题目内容
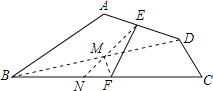
【题目】如图,在四边形ABCD中,BC、AD不平行,且∠BAD+∠ADC=270°,E、F分别是AD、BC的中点,已知EF=4,求AB2+CD2的值.

【答案】AB2+CD2=64.
【解析】
试题分析:连接BD,取BD的中点M,连接EM并延长交BC于N,连接FM,根据三角形中位线定理得到EM=![]() AB,FM=
AB,FM=![]() CD,∠NMF=90°,根据勾股定理计算即可.
CD,∠NMF=90°,根据勾股定理计算即可.
解:连接BD,取BD的中点M,连接EM并延长交BC于N,连接FM,
∵∠BAD+∠ADC=270°,
∴∠ABC+∠C=90°,
∵E、F、M分别是AD、BC、BD的中点,
∴EM∥AB,FM∥CD,EM=![]() AB,FM=
AB,FM=![]() CD,
CD,
∴∠MNF=∠ABC,∠MFN=∠C,
∴∠MNF+∠MFN=90°,即∠NMF=90°,
由勾股定理得,ME2+MF2=EF2=16,
∴AB2+CD2=(2ME)2+(2MF)2=64.

【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?
【题目】有这样一个问题:探究函数y=﹣ ![]() +|x|的图象与性质. 小军根据学习函数的经验,对函数y=﹣
+|x|的图象与性质. 小军根据学习函数的经验,对函数y=﹣ ![]() +|x|的图象与性质进行了探究.
+|x|的图象与性质进行了探究.
下面是小军的探究过程,请补充完整:
(1)函数y=﹣ ![]() +|x|的自变量x的取值范围是;
+|x|的自变量x的取值范围是;
(2)表是y与x的几组对应值
x | ﹣2 | ﹣1.9 | ﹣1.5 | ﹣1 | ﹣0.5 | 0 | 1 | 2 | 3 | 4 | … |
y | 2 | 1.60 | 0.80 | 0 | ﹣0.72 | ﹣1.41 | ﹣0.37 | 0 | 0.76 | 1.55 | … |
在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)观察图象,函数的最小值是;
(4)进一步探究,结合函数的图象,写出该函数的一条性质(函数最小值除外): .