题目内容
如图,抛物线y=-
x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于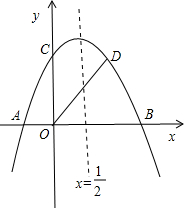 点C,对称轴为直线x=
点C,对称轴为直线x=
,OA=2,OD平分∠BOC交抛物线于点D(点D在第一象限).
(1)求抛物线的解析式和点D的坐标;
(2)在抛物线的对称轴上,是否存在一点P,使得△BPD的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)点M是抛物线上的动点,在x轴上是否存在点N,使A、D、M、N四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的M点坐标;如果不存在,请说明理由.
| 1 |
| 2 |
 点C,对称轴为直线x=
点C,对称轴为直线x=| 1 |
| 2 |
(1)求抛物线的解析式和点D的坐标;
(2)在抛物线的对称轴上,是否存在一点P,使得△BPD的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)点M是抛物线上的动点,在x轴上是否存在点N,使A、D、M、N四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的M点坐标;如果不存在,请说明理由.
(1)∵OA=2
∴A(-2,0)
∵A与B关于直线x=
对称
∴B(3,0),
由于A、B,两点在抛物线上,
∴
;
解得
;
∴y=-
x2+
x+3
过D作DE⊥x轴于E
∵∠BOC=90°,OD平分∠BOC
∴∠DOB=45°,∠ODE=45°,
∴DE=OE
即xD=yD,
∴x=-
x2+
x+3,
解得x1=2,x2=-3(舍去)
∴D(2,2);(4分)
(2)存在
∵BD为定值,
∴要使△BPD的周长最小,只需PD+PB最小
∵A与B关于直线x=
对称,
∴PB=PA,只需PD+PA最小
∴连接AD,交对称轴于点P,此时PD+PA最小,(2分)
由A(-2,0),D(2,2)可得
直线AD:y=
x+1(1分)
令x=
,y=
∴存在点P(
,
),使△BPD的周长最小(1分)
(3)存在.
(i)当AD为平行四边形AMDN的对角线时,MD∥AN,即MD∥x轴
∴yM=yD,
∴M与D关于直线x=
对称,
∴M(-1,2)(1分)
(ii)当AD为平行四边形ADNM的边时,
∵平行四边形ADNM是中心对称图形,△AND≌△ANM
∴|yM|=|yD|,
即yM=-yD=-2,
∴令-
x2+
x+3=-2,即x2-x-10=0;
解得x1,2=
,M(
,-2)或M(
,-2),(2分)
综上所述:满足条件的M点有三个M(-1,2),M(
,-2)或M(
,-2).(1分)
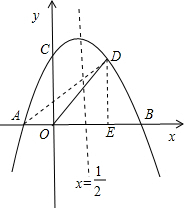
∴A(-2,0)
∵A与B关于直线x=
| 1 |
| 2 |
∴B(3,0),
由于A、B,两点在抛物线上,
∴
|
解得
|
∴y=-
| 1 |
| 2 |
| 1 |
| 2 |
过D作DE⊥x轴于E
∵∠BOC=90°,OD平分∠BOC
∴∠DOB=45°,∠ODE=45°,
∴DE=OE
即xD=yD,
∴x=-
| 1 |
| 2 |
| 1 |
| 2 |
解得x1=2,x2=-3(舍去)
∴D(2,2);(4分)
(2)存在
∵BD为定值,
∴要使△BPD的周长最小,只需PD+PB最小
∵A与B关于直线x=
| 1 |
| 2 |
∴PB=PA,只需PD+PA最小
∴连接AD,交对称轴于点P,此时PD+PA最小,(2分)
由A(-2,0),D(2,2)可得
直线AD:y=
| 1 |
| 2 |
令x=
| 1 |
| 2 |
| 5 |
| 4 |
∴存在点P(
| 1 |
| 2 |
| 5 |
| 4 |
(3)存在.
(i)当AD为平行四边形AMDN的对角线时,MD∥AN,即MD∥x轴
∴yM=yD,
∴M与D关于直线x=
| 1 |
| 2 |
∴M(-1,2)(1分)
(ii)当AD为平行四边形ADNM的边时,
∵平行四边形ADNM是中心对称图形,△AND≌△ANM
∴|yM|=|yD|,
即yM=-yD=-2,
∴令-
| 1 |
| 2 |
| 1 |
| 2 |
解得x1,2=
1±
| ||
| 2 |
1+
| ||
| 2 |
1-
| ||
| 2 |
综上所述:满足条件的M点有三个M(-1,2),M(
1+
| ||
| 2 |
1-
| ||
| 2 |


练习册系列答案
相关题目

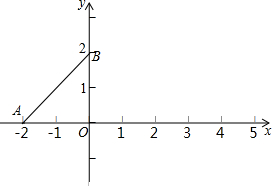 OC,(点A旋转到点B的位置),抛物线y=ax2+bx+c(a≠0)经过B,C两点,与x轴的另一个交点为点D,顶点为点P,对称轴为直线x=3,
OC,(点A旋转到点B的位置),抛物线y=ax2+bx+c(a≠0)经过B,C两点,与x轴的另一个交点为点D,顶点为点P,对称轴为直线x=3,

 及其内部的抛物线部分经过平移和对称变换得到的.
及其内部的抛物线部分经过平移和对称变换得到的.