题目内容
【题目】平面直角坐标系中,以点P(2,a)为圆心的⊙P与y轴相切,直线y=x与⊙P相交于点A、B,且AB的长为2![]() ,则a的值为_____.
,则a的值为_____.
【答案】2+![]() 或2﹣
或2﹣![]()
【解析】
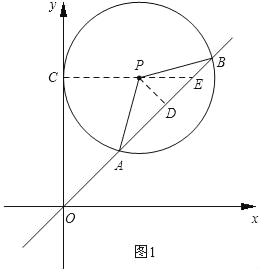
设⊙P与y轴相切于点C,连接PC,则有PC⊥OC,根据点P的坐标可得⊙P的半径PC为2,由于满足条件的点P可能在直线y=x的上方,也可能在直线y=x的下方,因此需分两种情况讨论.当点P在直线y=x上方时,如图1,连接CP并延长交直线y=x于点E,则有CE=OC.过点P作PD⊥AB于D,由垂径定理可求出AD,在Rt△ADP中,运用勾股定理可求出PD,在Rt△PDE中,运用三角函数可求出PE,就可求出a的值;当点P在直线y=x下方时,如图2,连接PC,过点P作PD⊥AB于D,过点P作x轴的垂线交x轴与点M,交AB于点N,
同理可得:OM=MN,PD=1,PN=![]() .易证四边形PCOM是矩形,从而有OM=PC=2,OC=PM,进而可以求出a的值,问题得以解决.
.易证四边形PCOM是矩形,从而有OM=PC=2,OC=PM,进而可以求出a的值,问题得以解决.
设⊙P与y轴相切于点C,连接PC,则有PC⊥OC.
∵点P的坐标为(2,a),∴PC=2.
①若点P在直线y=x上方,如图1,
连接CP并延长交直线y=x于点E,则有CE=OC.
∵CE⊥OC,CE=OC,
∴∠COE=∠CEO=45°.
过点P作PD⊥AB于D,
由垂径定理可得:AD=BD=![]() AB=
AB=![]() ×2
×2![]() =
=![]() .
.
在Rt△ADP中,
PD=![]() =1.
=1.
在Rt△PDE中,
sin∠PED=![]() ,
,
解得:PE=![]() .
.
∴OC=CE=CP+PE=2+![]() .
.
∴a=2+![]() .
.
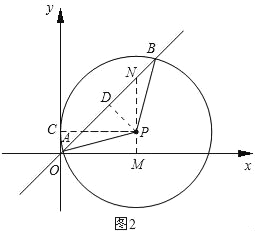
②若点P在直线y=x下方,如图2,
连接PC,过点P作PD⊥AB于D,
过点P作x轴的垂线交x轴与点M,交AB于点N,
同理可得:OM=MN,PD=1,PN=![]() .
.
∵∠PCO=∠COM=∠PMO=90°,
∴四边形PCOM是矩形.
∴OM=PC=2,OC=PM.
∴OC=PM=MN﹣PN=OM﹣PN=2﹣![]() .
.
∴a=2﹣![]() .
.
故答案为:2+![]() 或2﹣
或2﹣![]() .
.

 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案