题目内容
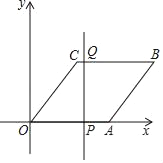
【题目】如图，在平面直角坐标系中，点A的坐标为（5，0），点B的坐标为（8，4），点C的坐标为（3，4），连接AB、BC、OC
（1）求证四边形OABC是菱形；
（2）直线l过点C且与y轴平行，将直线l沿x轴正方向平移，平移后的直线交x轴于点P．
①当OP：PA＝3：2时，求点P的坐标；
②点Q在直线1上，在直线l平移过程中，当△COQ是等腰直角三角形时，请直接写出点Q的坐标．
【答案】（1）证明见解析；（2）①点P坐标为（3，0）或（15，0）；②点Q坐标为：（﹣4，3），（7，1），（
，
）
【解析】
（1）根据两点距离公式可求AO=BC=CO=AB=5，即可证四边形OABC是菱形；
（2）①分点P在线段OA上，在点A右侧两种情况讨论，根据题意可求OP的长，即可求点P的坐标；
②分三种情况讨论，根据全等三角形的判定和性质，可求点Q的坐标．
证明：（1）∵点A的坐标为（5，0），点B的坐标为（8，4），点C的坐标为（3，4），O点坐标（0，0）
∴AO＝BC＝5，CO＝
＝5，AB＝
＝5
∴AO＝BC＝CO＝AB＝5
∴四边形ABCO是菱形
（2）①当点P在线段OA上，
∵OP：PA＝3：2，OP+AP＝5
∴OP＝3，PA＝2
∴点P坐标为（3，0）
当点P在点A的右侧，
∵OP：PA＝3：2，OP﹣AP＝OA＝5
∴OP＝15，AP＝10
∴点P坐标为（15，0）
②如图，当∠COQ＝90°，OC＝OQ时，过点C作CE⊥OA于E，则OE＝3，CE＝4，
∵∠COE+∠POQ＝90°，∠COE+∠OCE＝90°，
∴∠OCE＝∠POQ，且OC＝OQ，∠CEO＝∠OPQ
∴△COE≌△QOP（AAS）
∴PQ＝OE＝3，OP＝CE＝4，
∴点Q坐标（﹣4，3）
如图，当∠OCQ＝90°，OC＝CQ时，过点C作CE⊥OA于点E，则CE＝4，OE＝3，
过点Q作FQ⊥CE于点F，
∵∠OCE+∠ECQ＝90°，∠ECQ+∠CQF＝90°，
∴∠OCE＝∠CQF，且OC＝CQ，∠OEC＝∠CFQ＝90°，
∴△OEC≌△CFQ（AAS）
∴CF＝OE＝3，FQ＝CE＝4，
∴EF＝1，
∵QF⊥CE，CE⊥AO，PQ⊥OA
∴四边形EPQF是矩形
∴EP＝FQ＝4
即OP＝7
∴点Q坐标为（7，1）
如图，若∠CQO＝90°，CQ＝OQ时，过点C作CE⊥OA于点E，则CE＝4，OE＝3，
∵∠CQH+∠OQP＝90°，∠PQO+∠QOP＝90°，
∴∠CQH＝∠QOP，且OQ＝CQ，∠CHQ＝∠OPQ＝90°，
∴△OPQ≌△QHC（AAS）
∴OP＝HQ，CH＝PQ，
∵CE⊥OA，PH⊥BC，PH⊥OA
∴四边形CEPH是矩形，
∴EP＝CH＝PQ，HP＝CE＝4，
∵HQ+PQ＝HP＝4＝OP+EP，OP﹣EP＝OE＝3，
∴OP＝，EP＝PQ＝
∴点Q坐标（
）
综上所述：点Q坐标为：（﹣4，3），（7，1），（）
