题目内容
如图,沿AC的方向修建高速公路,为了加快工程进度,要在小山的两边同时施工.在AC上取一点B,在AC外另取一点D,使∠ABD=130°,BD=480 m,∠BDE=40°,问开挖点E离D多远,才能使A、C、E在一条直线上?(精确到0.1 m)

答案:
解析:
解析:
|
答:E离D点367.7 m.可使A、C、E在一条直线上. 解:连BE,在△BED中,∠D=40°,∠DBE=180°-∠ABD=180°-130°=50° ∴∠BED=90°. 在Rt△BDE中,BD=480. ∴ED=BD·sin50°=480×0.7660=367.68≈367.7(m) 思路点拨:设A、C、E共线,则△BDE为直角三角形. 在Rt△BDE中,BD=480,∠BDE=40.可求出ED. 评注:要排除题中无关因素的影响,看到问题的本质,由∠ABD=130°,∠BDE=40°,我们能得到∠BED=90°,这样我们就构造出了一个Rt△,这是解题的关键. 小结:由以上各中考题可见,对本节内容的考查主要集中在两个方面,一是用计算器求非特殊角的三角函数值.二是应用性问题.在应用性问题中构造适当的直角三角形是解题的关键. |

练习册系列答案
相关题目
 如图,沿AC方向开山修渠,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=135°,BD=520m,∠D=45°,如果要使A,C,E成一直线,求开挖点E离D的距离(精确到1m).
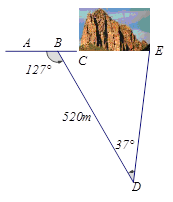
如图,沿AC方向开山修渠,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=135°,BD=520m,∠D=45°,如果要使A,C,E成一直线,求开挖点E离D的距离(精确到1m). (2012•吉林)如图,沿AC方向开山修一条公路,为了加快施工速度,要在小山的另一边寻找点E同时施工.从AC上的一点B取∠ABD=127°,沿BD的方向前进,取∠BDE=37°,测得BD=520m,并且AC,BD和DE在同一平面内.
(2012•吉林)如图,沿AC方向开山修一条公路,为了加快施工速度,要在小山的另一边寻找点E同时施工.从AC上的一点B取∠ABD=127°,沿BD的方向前进,取∠BDE=37°,测得BD=520m,并且AC,BD和DE在同一平面内.