题目内容
 (2012•吉林)如图,沿AC方向开山修一条公路,为了加快施工速度,要在小山的另一边寻找点E同时施工.从AC上的一点B取∠ABD=127°,沿BD的方向前进,取∠BDE=37°,测得BD=520m,并且AC,BD和DE在同一平面内.
(2012•吉林)如图,沿AC方向开山修一条公路,为了加快施工速度,要在小山的另一边寻找点E同时施工.从AC上的一点B取∠ABD=127°,沿BD的方向前进,取∠BDE=37°,测得BD=520m,并且AC,BD和DE在同一平面内.(1)施工点E离D多远正好能使成A,C,E一条直线(结果保留整数);
(2)在(1)的条件下,若BC=80m,求公路段CE的长(结果保留整数).
(参考数据:sin37°=0.60,cos37°=0.80,tan37°=0.75)
分析:(1)由若使A,C,E成一条直线,则需∠ABD是△BCE的外角,可求得∠E=90°,然后由DE=BD•cos37°,即可求得答案;
(2)首先由BE=BD•sin37°,求得BE的长,又由BC=80m,即可求得公路段CE的长.
(2)首先由BE=BD•sin37°,求得BE的长,又由BC=80m,即可求得公路段CE的长.
解答:解:(1)若使A,C,E成一条直线,
则需∠ABD是△BDE的外角,
∴∠E=∠ABD-∠D=127°-37°=90°,
∴DE=BD•cos37°=520×0.80=416(m)
∴施工点E离D距离为416m时,正好能使A,C,E成一条直线;
(2)由(1)得:在Rt△BED中,∠E=90°,
又∵∠D=37°,
∴BE=BD•sin37°=520×0.60=312(m),
∵BC=80m,
∴CE=BE-BC=312-80=232(m).
∴公路段CE的长为232m.
则需∠ABD是△BDE的外角,
∴∠E=∠ABD-∠D=127°-37°=90°,
∴DE=BD•cos37°=520×0.80=416(m)
∴施工点E离D距离为416m时,正好能使A,C,E成一条直线;
(2)由(1)得:在Rt△BED中,∠E=90°,
又∵∠D=37°,
∴BE=BD•sin37°=520×0.60=312(m),
∵BC=80m,
∴CE=BE-BC=312-80=232(m).
∴公路段CE的长为232m.
点评:此题考查了解直角三角形的应用问题.此题难度适中,解题的关键是把实际问题转化为数学问题求解,注意数形结合思想的应用.

练习册系列答案
相关题目
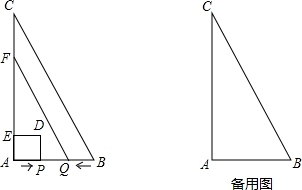 P为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.
P为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.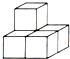 (2012•吉林)如图,有5个完全相同的小正方体组合成一个立方体图形,它的俯视图是( )
(2012•吉林)如图,有5个完全相同的小正方体组合成一个立方体图形,它的俯视图是( ) (2012•吉林)如图,在△ABC中,∠A=80°,∠B=40°.D、E分别是AB,AC上的点,且DE∥BC,则∠AED的度数是( )
(2012•吉林)如图,在△ABC中,∠A=80°,∠B=40°.D、E分别是AB,AC上的点,且DE∥BC,则∠AED的度数是( )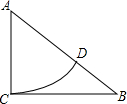 (2012•吉林)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点A为圆心,AC长为半径画弧,交AB于点D,则BD=
(2012•吉林)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点A为圆心,AC长为半径画弧,交AB于点D,则BD=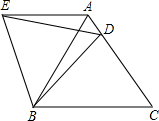 (2012•吉林)如图,在等边△ABC中,D是边AC上一点,连接BD.将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=10,BD=9,则△AED的周长是
(2012•吉林)如图,在等边△ABC中,D是边AC上一点,连接BD.将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=10,BD=9,则△AED的周长是