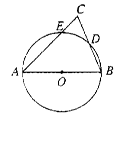
题目内容
如图,以BC为直径的⊙O1与⊙O2外切,⊙O1与⊙O2的外公切线交于点D,且∠ADC=60°,过B点的⊙O1的切线交其中一条外公切线于点A.若⊙O2的面积为π,则四边形ABCD的面积是 .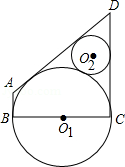

12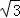
解:∵⊙O2的面积为π,
∴⊙O2的半径是1,
∵AB和AH是⊙O1的切线,
∴AB=AH,
设⊙O2的半径是R,
连接DO2,DO1,O2E,O1H,AO1,作O2F⊥BC于F,
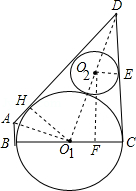
∵⊙O1与⊙O2外切,⊙O1与⊙O2的外公切线DC.DA,∠ADC=60°,
∴D.O2、O1三点共线,∠CDO1=30°,
∴∠DAO1=60°,∠O2EC=∠ECF=∠CFO2=90°,
∴四边形CFO2E是矩形,
∴O2E=CF,CE=FO2,∠FO2O1=∠CDO1=30°,
∴DO2=2O2E=2,∠HAO1=60°,R+1=2(R﹣1),
解得:R=3,
即DO1=2+1+3=6,
在Rt△CDO1中,由勾股定理得:CD=3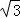 ,
,
∵∠HO1A=90°﹣60°=30°,HO1=3,
∴AH=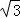 =AB,
=AB,
∴四边形ABCD的面积是: ×(AB+CD)×BC=
×(AB+CD)×BC= ×(
×(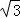 +3
+3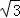 )×(3+3)=12
)×(3+3)=12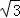 .
.
∴⊙O2的半径是1,
∵AB和AH是⊙O1的切线,
∴AB=AH,
设⊙O2的半径是R,
连接DO2,DO1,O2E,O1H,AO1,作O2F⊥BC于F,

∵⊙O1与⊙O2外切,⊙O1与⊙O2的外公切线DC.DA,∠ADC=60°,
∴D.O2、O1三点共线,∠CDO1=30°,
∴∠DAO1=60°,∠O2EC=∠ECF=∠CFO2=90°,
∴四边形CFO2E是矩形,
∴O2E=CF,CE=FO2,∠FO2O1=∠CDO1=30°,
∴DO2=2O2E=2,∠HAO1=60°,R+1=2(R﹣1),
解得:R=3,
即DO1=2+1+3=6,
在Rt△CDO1中,由勾股定理得:CD=3
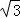 ,
,∵∠HO1A=90°﹣60°=30°,HO1=3,
∴AH=
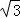 =AB,
=AB,∴四边形ABCD的面积是:
 ×(AB+CD)×BC=
×(AB+CD)×BC= ×(
×(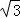 +3
+3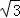 )×(3+3)=12
)×(3+3)=12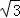 .
.
练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 ,点
,点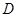 是母线
是母线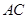 的中点,一只蚂蚁从点
的中点,一只蚂蚁从点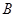 出发沿圆锥的表面爬行到点
出发沿圆锥的表面爬行到点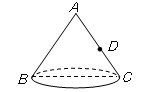
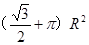
 等表示;
等表示; 等表示;
等表示;
 弧AE=弧BE ; ④2CE·AB=BC2,
弧AE=弧BE ; ④2CE·AB=BC2,