题目内容
【题目】
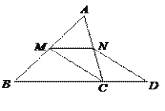
已知：如图，在△ABC中，M是边AB的中点，D是边BC延长线上一点，
，DN∥CM，交边AC于点N．
（1）求证：MN∥BC；
（2）当∠ACB为何值时，四边形BDNM是等腰梯形？并证明你的猜想．
【答案】（1）见解析；
（2）当∠ACB=90°时，四边形BDNM是等腰梯形．
证明见解析．
【解析】
（1）证法一：取边BC的中点E，联结ME．
∵BM=AM，BE=EC，∴ME∥AC．
∴∠MEC=∠NCD．
∵
，∴
．
∵DN∥CM，∴∠MCE=∠D．
∴△MEC≌△NCD．
∴
．
又∵CM∥DN，∴四边形MCDN是平行四边形．
∴MN∥BC．
证法二：延长CD到F，使得
，联结AF．
∵，
，∴
．
∵
，∴MC∥AF．
∵MC∥DN，∴ND∥AF．
又∵，∴
．
∴MN∥BC．
（2）解：当∠ACB=90°时，四边形BDNM是等腰梯形．
证明如下：
∵MN∥BD，BM与DN不平行，∴四边形BDNM是梯形．
∵∠ACB=90°，，∴
．
∵，∴BM
DN．
∴四边形BDNM是等腰梯形．
练习册系列答案
相关题目
【题目】为了倡导节约能源，自某日起，我国对居民用电采用阶梯电价，为了使大多数家庭不增加电费支出，事前就需要了解居民全年月平均用电量的分布情况，制订一个合理的方案.某调查人员随机调查了
市
户居民全年月平均用电量(单位：千瓦时)数据如下：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
得到如下频数分布表：
全年月平均用电量/千时 | 频数 | 频率 |
|
|
|
| ||
| ||
|
| |
|
| |
|
| |
合计 |
|
|
画出频数分布直方图，如下：
(1)补全数分布表和率分布直方图
(2)若是根据数分布表制成扇形统计图，则不低于
千瓦时的部分圆心角的度数为_____________；
(3)若市的阶梯电价方案如表所示，你认为这个阶梯电价方案合理吗?
档次 | 全年月平均用电量/千瓦时 | 电价(元/千瓦时) |
第一档 |
|
|
第二档 |
|
|
第三档 | 大于 |
|
