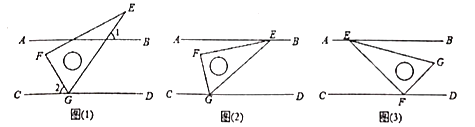
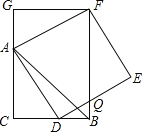
题目内容
【题目】实验中学学生在学习等腰三角形性质“三线合一”时
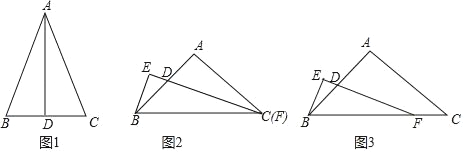
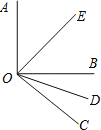
(1)(探究发现)如图1,在△ABC中,若AD平分∠BAC,AD⊥BC时,可以得出AB=AC,D为BC中点,请用所学知识证明此结论.
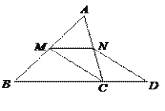
(2)(学以致用)如果Rt△BEF和等腰Rt△ABC有一个公共的顶点B,如图2,若顶点C与顶点F也重合,且∠BFE=![]() ∠ACB,试探究线段BE和FD的数量关系,并证明.
∠ACB,试探究线段BE和FD的数量关系,并证明.
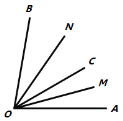
(3)(拓展应用)如图3,若顶点C与顶点F不重合,但是∠BFE=![]() ∠ACB仍然成立,(学以致用)中的结论还成立吗?证明你的结论.
∠ACB仍然成立,(学以致用)中的结论还成立吗?证明你的结论.
【答案】(1)见解析;(2)结论:DF=2BE;(3)结论不变:DF=2BE.
【解析】
(1)只要证明△ADB≌△ADC(ASA)即可.
(2)结论:DF=2BE.如图2中,延长BE交CA的延长线于K.想办法证明△BAK≌△CAD(ASA)即可解决问题.
(3)如图3中,结论不变:DF=2BE.作FK∥CA交BE的延长线于K,交AB于J.利用(2)中结论证明即可.
解:(1)如图1中,

∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵DA平分∠BAC,
∴∠DAB=∠DAC,
∵AD=AD,
∴△ADB≌△ADC(ASA),
∴AB=AC,BD=DC.
(2)结论:DF=2BE.
理由:如图2中,延长BE交CA的延长线于K.
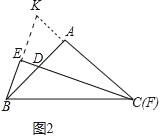
∵CE平分∠BCK,CE⊥BK,
∴由(1)中结论可知:CB=CK,BE=KE,
∵∠∠BAK=∠CAD=∠CEK=90°,
∴∠ABK+∠K=90°,∠ACE+∠K=90°,
∴∠ABK=∠ACD,
∵AB=AC,
∴△BAK≌△CAD(ASA),
CD=BK,
∴CD=2BE,即DF=2BE.
(3)如图3中,结论不变:DF=2BE.

理由:作FK∥CA交BE的延长线于K,交AB于J.
∵FK∥AC,
∴∠FJB=∠A=90°,∠BFK=∠BCA,
∵∠JBF=45°,
∴△BJF是等腰直角三角形,
∵∠BFE=![]() ACB,
ACB,
∴∠BFE=![]() ∠BFJ,
∠BFJ,
由(2)可知:DF=2BE.

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.