ƒøƒ⁄»›
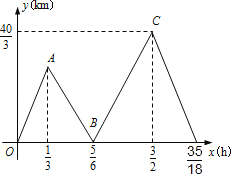
°æƒø°øº◊∆ÔµÁ∂Ø≥µ°¢““∆Ôƒ¶Õ–≥µ∂º¥”Mµÿ≥ˆ∑¢£¨—ÿ“ªÃı± ÷±µƒπ´¬∑‘»ÀŸ«∞Õ˘Nµÿ£¨º◊œ»≥ˆ∑¢“ª∂Œ ±º‰∫Û““‘Ÿ≥ˆ∑¢£¨º◊°¢““¡Ω»ÀµΩ¥ÔNµÿ∫Ûæ˘Õ£÷π∆Ô––£Æ“—÷™M°¢N¡Ωµÿœ‡æ‡![]() km£¨…˺◊–– ªµƒ ±º‰Œ™x£®h£©£¨º◊°¢““¡Ω»À÷ƺ‰µƒæ‡¿ÎŒ™y£®km£©£¨±Ì æy”Îx∫Ø ˝πÿœµµƒ≤ø∑÷ÕºœÛ»ÁÕºÀ˘ æ£Æ«Îƒ„Ω‚æˆ“‘œ¬Œ £∫
km£¨…˺◊–– ªµƒ ±º‰Œ™x£®h£©£¨º◊°¢““¡Ω»À÷ƺ‰µƒæ‡¿ÎŒ™y£®km£©£¨±Ì æy”Îx∫Ø ˝πÿœµµƒ≤ø∑÷ÕºœÛ»ÁÕºÀ˘ æ£Æ«Îƒ„Ω‚æˆ“‘œ¬Œ £∫

£®1£©«Ûœfl∂ŒBCÀ˘‘⁄÷±œflµƒ∫Ø ˝±Ì¥Ô Ω£ª
£®2£©«Ûµ„Aµƒ◊¯±Í£¨≤¢Àµ√˜µ„Aµƒ µº “‚“£ª
£®3£©∏˘æ›Ã‚ƒø–≈œ¢≤π»´∫Ø ˝ÕºœÛ£Æ£®–αÍ√˜œ‡πÿ ˝æ›£©
°æ¥∞∏°ø£®1£©y£Ω20x©Å![]() £ª£®2£©µ„Aµƒ µº “‚“ «µ±º◊∆ÔµÁ∂Ø≥µ–– ª
£ª£®2£©µ„Aµƒ µº “‚“ «µ±º◊∆ÔµÁ∂Ø≥µ–– ª![]() ±£¨æ‡¿ÎMµÿŒ™10 km£ª£®3£©º˚Ω‚Œˆ
±£¨æ‡¿ÎMµÿŒ™10 km£ª£®3£©º˚Ω‚Œˆ
°æΩ‚Œˆ°ø
£®1£©∏˘æ›∫Ø ˝ÕºœÛ÷–µƒ ˝æ›ø…“‘«Ûµ√œfl∂ŒBCÀ˘‘⁄÷±œflµƒ∫Ø ˝±Ì¥Ô Ω£ª
£®2£©∏˘æ›Ã‚“‚∫Õ∫Ø ˝ÕºœÛ÷–µƒ ˝æ›ø…“‘«Ûµ√º◊∫Õ““µƒÀŸ∂»£¨¥”∂¯ø…“‘«Ûµ√µ„Aµƒ◊¯±Í≤¢–¥≥ˆµ„A±Ì 浃 µº “‚“£ª
£®3£©∏˘æ›£®2£©÷–º◊““µƒÀŸ∂»ø…“‘∑÷±«Ûµ√º◊““¥”MµÿµΩNµÿ”√µƒ ±º‰£¨¥”∂¯ø…“‘Ω´∫Ø ˝ÕºœÛ≤π≥‰ÕÍ’˚£Æ
Ω‚£∫£®1£©…Ëœfl∂ŒBCÀ˘‘⁄÷±œflµƒ∫Ø ˝±Ì¥Ô ΩŒ™y£Ωkx+b£®k°Ÿ0£©£¨
°flB£®![]() £¨0£©£¨C£®
£¨0£©£¨C£®![]() £¨
£¨![]() £©‘⁄÷±œflBC…œ£¨
£©‘⁄÷±œflBC…œ£¨
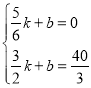 £¨µ√
£¨µ√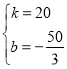 £¨
£¨
º¥œfl∂ŒBCÀ˘‘⁄÷±œflµƒ∫Ø ˝±Ì¥Ô ΩŒ™y£Ω20x©Å![]() £ª
£ª
£®2£©…˺◊µƒÀŸ∂»Œ™m km/h£¨““µƒÀŸ∂»Œ™n km/h£¨
 £¨µ√
£¨µ√![]() £¨
£¨
°‡µ„Aµƒ◊›◊¯±Í «£∫30°¡![]() £Ω10£¨
£Ω10£¨
º¥µ„Aµƒ◊¯±ÍŒ™£®![]() £¨10£©£¨
£¨10£©£¨
µ„Aµƒ µº “‚“ «µ±º◊∆ÔµÁ∂Ø≥µ–– ª![]() ±£¨æ‡¿ÎMµÿŒ™10 km£ª
±£¨æ‡¿ÎMµÿŒ™10 km£ª
£®3£©”…£®2£©ø…÷™£¨º◊µƒÀŸ∂»Œ™30km/h£¨““µƒÀŸ∂»Œ™50«ß√◊/–° ±£¨
‘Ú““¥”MµÿµΩ¥ÔNµÿ”√µƒ ±º‰Œ™£∫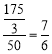 –° ±£¨
–° ±£¨
°fl![]() £¨
£¨
°‡““‘⁄ÕºœÛ÷–µƒ![]() ±£¨Õ£÷π‘À∂Ø£¨
±£¨Õ£÷π‘À∂Ø£¨
º◊µΩ¥ÔNµÿ”√µƒ ±º‰Œ™£∫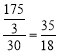 –° ±£¨
–° ±£¨
≤π»´µƒ∫Ø ˝ÕºœÛ»Á”“ÕºÀ˘ æ£Æ

 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏