Question

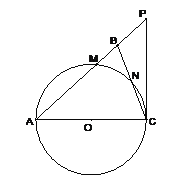
【题目】如图，在△ABC中，∠ABC=∠ACB，以AC为直径的⊙O分别交AB、BC于点M、N，点P在AB的延长线上，且∠CAB=2∠BCP.

（1）求证：直线CP是⊙O的切线；

（2）若BC=2，sin∠BCP=，求⊙O的半径及△ACP的周长.

Answer 1

【答案】详见解析.

【解析】试题分析: （1）欲证明直线CP是的切线，只需证得CP⊥AC；
（2）利用正弦三角函数的定义求得 的直径则 的半径为

如图，过点B作BD⊥AC于点D，构建相似三角形：△CAN∽△CBD，所以根据相似三角形的对应边成比例求得线段；然后在Rt△BCD中,，利用勾股定理可以求得 所以利用平行线分线段成比例分别求得线段的长度．即可求出的周长．

试题解析：(1)证明：连接AN，

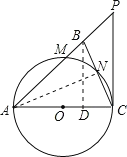
∵∠ABC=∠ACB，∴AB=AC，

∵AC是的直径，∴AN⊥BC，

∴∠CAN=∠BAN，BN=CN，

∵∠CAB=2∠BCP，

∴∠CAN=∠BCP.

∵∠CAN+∠ACN=，

∴∠BCP+∠ACN=，

∴CP⊥AC,

∵OC是的半径

∴CP是的切线；

(2)

∴AC=5，

∴的半径为

如图，过点B作BD⊥AC于点D.

由(1)得

在Rt△CAN中,

在△CAN和△CBD中，

∴△CAN∽△CBD，

∴BD=4.

在Rt△BCD中,

∴AD=ACCD=52=3，

∵BD∥CP，

∴△APC的周长是AC+PC+AP=20.