题目内容
【题目】已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.
(1)旋转中心是 .旋转角为 度.
(2)请你判断△DFE的形状,并说明理由.
(3)求四边形DEBF的周长和面积.
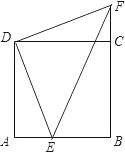
【答案】(1)D,90;(2) △DFE的形状是等腰直角三角形,见解析;(3)20,16
【解析】
(1)由题意可知要确定旋转中心及旋转的角度,首先确定哪是对应点,即可确定旋转中心以及旋转角;
(2)根据旋转的性质,可以得到旋转前后的两个图形全等,以及旋转角的定义即可作出判断;
(3)由题意根据△DAE≌△DCF,可以得到:AE=CF,DE=DF,则四边形DEBF的周长就是正方形的三边的和与DE的和.
解:(1)由题意可知旋转中心是点D,
![]() 即为旋转角为90度.
即为旋转角为90度.
(2)根据旋转的性质可得:△DAE≌△DCF,则DE=DF,∠EDF=∠ADC=90°,
则△DFE的形状是等腰直角三角形.
(3)四边形DEBF的周长是BE+BC+CF+DF+DE=AB+BC+DE+DF=4+4+6+6=20;
由题意可知四边形DEBF的面积等于正方形ABCD的面积=16.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目