Question

【题目】如图，在△ABC中，三个内角的平分线AD、BM、CN交于点O，OE⊥BC于点E．

（1）求∠ABO+∠BCO+∠CAO的度数；
（2）∠BOD与∠COE是否相等？请说明理由．

Answer 1

【答案】
（1）解：∵AD、BM、CN是△ABC三个内角的平分线，

∴∠BAO=∠CAO= ∠BAC，∠ABO=∠CBO= ∠ABC，∠ACO=∠BCO= ∠ACB，

∴∠ABO+∠BCO+∠CAO= （∠ABC+∠ACB+∠BAC）．

∵∠ABC+∠ACB+∠BAC=360°，

∴∠ABO+∠BCO+∠CAO=90°．

（2）解：∠BOD=∠COE，理由如下：

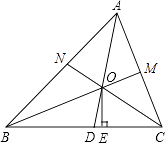
∵∠BOD是△ABO的外角，

∴∠BOD=∠ABO+∠BAO= （∠ABC+∠BAC）= （180°﹣∠ACB）=90°﹣ ∠ACB．

∵OE⊥BC，

∴∠COE+∠BCO=90°，

∴∠COE=90°﹣∠BCO=90°﹣ ∠ACB．

∴∠BOD=∠COE．

【解析】（1）根据角平分线的定义可得∠BAO=∠CAO=∠BAC、∠ABO=∠CBO=∠ABC、∠ACO=∠BCO=∠ACB，结合三角形的内角和可得∠ABO+∠BCO+∠CAO=（∠ABC+∠ACB+∠BAC）=90°；
（2）根据三角形外角的性质可得∠BOD=∠ABO+∠BAO=90°-∠ACB，由OE⊥BC结合三角形内角和可得出∠COE=90°-∠BCO=90°-∠ACB，进而可得出∠BOD=∠COE.
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识，掌握三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角．