题目内容
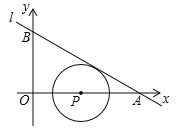
【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：
与x轴、y轴分别交于A、B，∠OAB=30°，点P在x轴上，⊙P与l相切，当P在线段OA上运动时，使得⊙P成为整圆的点P个数是（ ）
A．6 B．8 C．10 D．12
【答案】A．
【解析】
试题分析：∵直线l：
与x轴、y轴分别交于A、B，∴B（0，
），∴OB=
，在RT△AOB中，∠OAB=30°，∴OA=
OB=
=12，∵⊙P与l相切，设切点为M，连接PM，则PM⊥AB，∴PM=
PA，设P（x，0），∴PA=12﹣x，∴⊙P的半径PM=PA=
，∵x为整数，PM为整数，∴x可以取0，2，4，6，8，10，共6个数，∴使得⊙P成为整圆的点P个数是6．故选A．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
