题目内容
【题目】A，B两地相距200千米，甲车从A地出发匀速行驶到B地，乙车从B地出发匀速行驶到A地．乙车行驶1小时后，甲车出发，两车相向而行．设行驶时间为x小时（0≤x≤5），甲、乙两车离A地的距离分别为y1，y2千米，y1，y2与x之间的函数关系图象如图1所示．根据图象解答下列问题：
（1）求y1，y2与x的函数关系式；
（2）乙车出发几小时后，两车相遇？相遇时，两车离A地多少千米？
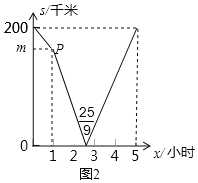
（3）设行驶过程中，甲、乙两车之间的距离为s千米，在图2的直角坐标系中，已经画出了s与x之间的部分函数图象．
①图中点P的坐标为（1，m），则m＝ ；
②求s与x的函数关系式，并在图2中补全整个过程中s与x之间的函数图象．
【答案】（1）y1＝50x﹣50，y2＝﹣40x+200；（2）乙车出发
小时后，两年相遇，相遇时，两车离A地
千米；（3）①160；②当1≤x≤时，s＝250﹣90x；当＜x≤5时，s＝90x﹣250；图象详见解析.
【解析】
（1）用待定系数法可求解析式；（2）将两个函数表达式组成方程组可求解；（3）①由点P表达的意义可求m的值；②分相遇前和相遇后两种情况分别求解析式．
解：（1）如图1，甲的图象过点（1，0），（5，200），
∴设甲的函数表达式为：y1＝kx+b，
∴
解得：
∴甲的函数表达式为：y1＝50x﹣50，
如图1，乙的图象过点（5，0），（0，200），
∴设乙的函数表达式为：y2＝mx+200，
∴0＝5m+200
∴m＝﹣40，
∴乙的函数表达式为：y2＝﹣40x+200，
（2）由题意可得：
解得：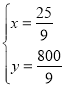
答：乙车出发小时后，两年相遇，相遇时，两车离A地千米．
（3）①由题意可得乙先出发1小时，且速度为40千米/小时，
∴m＝200﹣40×1＝160，
故答案为160；
②当1≤x≤时，s＝200﹣40×1﹣（40+50）（x﹣1）＝250﹣90x；
当＜x≤5时，s＝90x﹣250；
图象如下：
