Question

  如图，在Rt△ABC中，∠ACB=90°，M为AB边的中点，将Rt△ABC绕点M旋转，使点A与点C重合得到△CED，连结MD．若∠B=26°，则∠BMD等于(      )

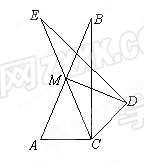
A．76°

B．96°

C．52°

D．104°

Answer 1

A

分析：先根据直角三角形两锐角互余，由∠B=26°得出∠A=64°，再根据直角三角形斜边上的中线等于斜边的一半得出MA=MC，由等角对等边及三角形内角和定理得出∠AMC=52°，然后根据旋转的性质得出△ACM≌△CDM，则∠AMC=∠CMD=52°，从而由平角的定义得出∠BMD的度数．

解：在Rt△ABC中，∵∠ACB=90°，∠B=26°，
∴∠A=64°，
又∵M为AB边的中点，
∴CM=AM，
∴∠ACM=∠A=64°，
∴∠AMC=180°-∠ACM-∠A=52°．
∵将Rt△ABC绕点M旋转，使点A与点C重合得到△CED，
∴△ACM≌△CDM，
∴∠AMC=∠CMD=52°，
∴∠BMD=180°-∠AMC-∠CMD=76°．
故选A．