题目内容
【题目】已知二次函数y=﹣ ![]() ﹣7x+
﹣7x+ ![]() ,若自变量x分别取x1 , x2 , x3 , 且﹣13<x1<0,x3>x2>2,则对应的函数值y1 , y2 , y3的大小关系正确的是( )
,若自变量x分别取x1 , x2 , x3 , 且﹣13<x1<0,x3>x2>2,则对应的函数值y1 , y2 , y3的大小关系正确的是( )
A.y1>y2>y3
B.y1<y2<y3
C.y2>y3>y1
D.无法确定
【答案】A
【解析】解:当y=0时,﹣ ![]() ﹣7x+
﹣7x+ ![]() =0,
=0,
解得:x=﹣15或x=1,
即抛物线与x轴的交点为(﹣15,0)、(1,0),
∵y=﹣ ![]() ﹣7x+
﹣7x+ ![]() =﹣
=﹣ ![]() (x+7)2+32,
(x+7)2+32,
∵a<0
∴当x>﹣7时,y随x的增大而减小,
∵x3>x2>2
∴y3<y2<0,
∵﹣13<x1<0,而-15<﹣13<-7,
∴y1>0
∴y1>y2>y3。
所以答案是:A.
【考点精析】利用二次函数的性质和抛物线与坐标轴的交点对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.

【题目】在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
阅读时间(小时) | 频数(人) | 频率 |
1≤x<2 | 18 | 0.12 |
2≤x<3 | a | m |
3≤x<4 | 45 | 0.3 |
4≤x<5 | 36 | n |
5≤x<6 | 21 | 0.14 |
合计 | b | 1 |
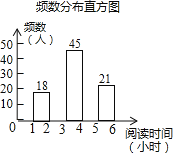
(1)填空:a= ,b= ,m= ,n= ;
(2)将频数分布直方图补充完整(画图后请标注相应的频数).