题目内容
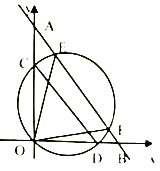
【题目】如图,在平面直角坐标系中,直线![]() 交y轴于点A,交x轴于点B,点C在线段OA上,点D在线段OB上,且
交y轴于点A,交x轴于点B,点C在线段OA上,点D在线段OB上,且![]() ,点C、D不与点O重合,以CD为直径的圆交直线AB于两点E、F,连接OE、OF,则当
,点C、D不与点O重合,以CD为直径的圆交直线AB于两点E、F,连接OE、OF,则当![]() 的面积的最大时,线段EF的长是________.
的面积的最大时,线段EF的长是________.
【答案】4.8
【解析】
根据题意可求出![]() 的长,利用面积法可求得EF边上的高,当
的长,利用面积法可求得EF边上的高,当![]() 的面积的最大时,线段EF的长也是最大的,弦大,则弦心距小,所以EF边上的高与EF的弦心距共线时,弦心距最小,如图,在Rt
的面积的最大时,线段EF的长也是最大的,弦大,则弦心距小,所以EF边上的高与EF的弦心距共线时,弦心距最小,如图,在Rt![]() 中,利用勾股定理可求得弦EF的长.
中,利用勾股定理可求得弦EF的长.
由题意得![]() ,
,![]()
∴![]() 则
则![]() ,
,
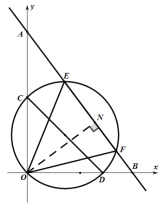
如图,过O作![]() 于N,
于N,
∵![]() ,即
,即![]()
∴![]() 4.8
4.8
![]()
![]() 最大,则
最大,则![]() 最大,
最大,
![]() 是圆中的弦,弦
是圆中的弦,弦![]() 最大,则弦心距
最大,则弦心距![]() 最小,如图:
最小,如图:
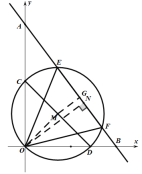
![]() ,
,
∵![]() 在以O为圆心,3为半径的圆上,
在以O为圆心,3为半径的圆上,
∴当![]() 在同一直线上时,
在同一直线上时,![]() 最小,如图:
最小,如图:
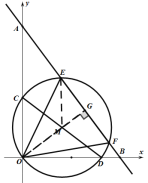
![]()
连接![]() ,在Rt
,在Rt![]() 中,
中,
![]()
根据垂径定理得:![]()
故答案为:4.8.

练习册系列答案
相关题目