��Ŀ����
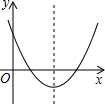
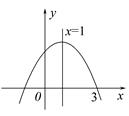
��ͼ1����֪������C����ԭ�㣬�Գ���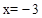 ���������ཻ�ڵ������ĵ�M����x���ཻ�ڵ�N����
���������ཻ�ڵ������ĵ�M����x���ཻ�ڵ�N���� ��
��

��1����������C�Ľ���ʽ��
��2����������C��ԭ��O��ת1800�õ�������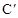 ��������
��������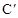 ��x�����һ����ΪA��BΪ������
��x�����һ����ΪA��BΪ������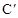 �Ϻ�����Ϊ2�ĵ㡣
�Ϻ�����Ϊ2�ĵ㡣
����PΪ�߶�AB��һ���㣬PD��y���ڵ�D�����APD��������ֵ��
�ڹ��߶�OA�ϵ�����E��F�ֱ���x��Ĵ��ߣ�������O��B��A��E1��F1���ٷֱ����߶�EE1��FF1Ϊ������ͼ2��ʾ�ĵȱߡ�AE1E2���ȱߡ�AF1F2����E��ÿ��1�����ȵ�λ���ٶȴӵ�O���A�˶�����F��ÿ��1�����ȵ�λ���ٶȴӵ�A���O�˶�������AE1E2��һ�����AF1F2��ijһ����ͬһֱ����ʱ����ʱ��t��ֵ��
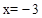 ���������ཻ�ڵ������ĵ�M����x���ཻ�ڵ�N����
���������ཻ�ڵ������ĵ�M����x���ཻ�ڵ�N���� ��
��
��1����������C�Ľ���ʽ��
��2����������C��ԭ��O��ת1800�õ�������
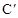 ��������
��������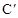 ��x�����һ����ΪA��BΪ������
��x�����һ����ΪA��BΪ������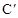 �Ϻ�����Ϊ2�ĵ㡣
�Ϻ�����Ϊ2�ĵ㡣����PΪ�߶�AB��һ���㣬PD��y���ڵ�D�����APD��������ֵ��
�ڹ��߶�OA�ϵ�����E��F�ֱ���x��Ĵ��ߣ�������O��B��A��E1��F1���ٷֱ����߶�EE1��FF1Ϊ������ͼ2��ʾ�ĵȱߡ�AE1E2���ȱߡ�AF1F2����E��ÿ��1�����ȵ�λ���ٶȴӵ�O���A�˶�����F��ÿ��1�����ȵ�λ���ٶȴӵ�A���O�˶�������AE1E2��һ�����AF1F2��ijһ����ͬһֱ����ʱ����ʱ��t��ֵ��
�⣺��1���������ߵĶԳ���Ϊ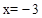 ����ON=3��
����ON=3��
�� ����NM=9����M����3����9����
����NM=9����M����3����9����
����������C�Ľ���ʽΪ ��
��
��������C����ԭ�㣬��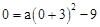 ����
����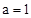 ��
��
��������C�Ľ���ʽΪ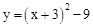 ����
���� ��
��
��2���١�������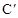 ��������C��ԭ��O��ת1800�õ���
��������C��ԭ��O��ת1800�õ���
��������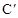 ��������C����ԭ��O�Գơ���������
��������C����ԭ��O�Գơ���������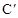 �Ķ�������Ϊ��3��9����
�Ķ�������Ϊ��3��9����
��������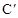 �Ľ���ʽΪ
�Ľ���ʽΪ ����
����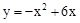 ��
��
����y=0����x=0��x=6����A��6��0����
�֡�BΪ������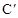 �Ϻ�����Ϊ2�ĵ㣬����x=2����y=8����B��2��8����
�Ϻ�����Ϊ2�ĵ㣬����x=2����y=8����B��2��8����
��ֱ��AB�Ľ���ʽΪy=kx+b��
��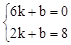 ����ã�
����ã�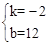 ��
��
��ֱ��AB�Ľ���ʽΪ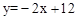 ��
��
��PΪ�߶�AB��һ���㣬����P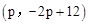 ��
��
��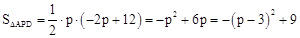 ��
��
APD��������ֵΪ9��
����ͼ���ֱ��E2��F2��x��Ĵ��ߣ�����ֱ�ΪG��H��
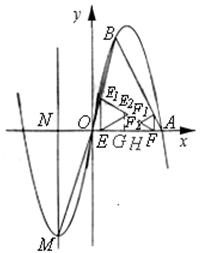
����ֱ��OB��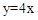 ���ɢ�ֱ��AB��
���ɢ�ֱ��AB��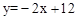 ��
��
��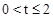 ʱ��E1��OB�ϣ�F1��AB�ϣ�
ʱ��E1��OB�ϣ�F1��AB�ϣ�
OE=t��EE1=4t��EG=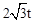 ��OG=
��OG=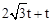 ��GE2=2t��
��GE2=2t��
OF=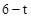 ��FF1=2t��HF=
��FF1=2t��HF=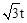 ��OH=
��OH=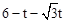 ��HF2= t��
��HF2= t��
��E��t��0����E1��t��4t����E2��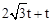 ��2t����F��6��t��0����F1��
��2t����F��6��t��0����F1��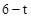 ��2t����F2��
��2t����F2��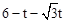 ��t����
��t����
i����EE1��FF1��ͬһֱ���ϣ���t=6��t��t=3��������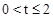 ��
��
ii����EE2��F1F2��ͬһֱ���ϣ������EE2��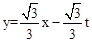 ����F1��
����F1��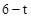 ��2t�����룬��
��2t�����룬��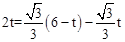 �����
�����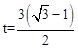 ��
��
iii����E1E2��FF2��ͬһֱ���ϣ������E1E2��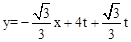 ����F��
����F��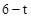 ��0�����룬��
��0�����룬��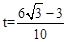 ��
��
��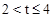 ʱ��E1��F1����AB�ϣ�
ʱ��E1��F1����AB�ϣ�
OE=t��EE1=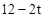 ��EG=
��EG=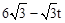 ��OG=
��OG=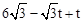 ��GE2=
��GE2=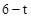 ��
��
OF=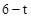 ��FF1=2t��HF=
��FF1=2t��HF=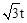 ��OH=
��OH=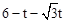 ��HF2= t��
��HF2= t��
��E��t��0����E1��t��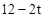 ����E2��
����E2��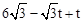 ��
��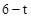 ����F��
����F��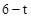 ��0����F1��
��0����F1��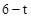 ��2t����F2��
��2t����F2��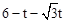 ��t����
��t����
i����EE1��FF1��ͬһֱ���ϣ���t=6��t��t=3��
ii����EE2��F1F2��ͬһֱ���ϣ������EE2��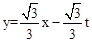 ����F1��
����F1��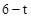 ��2t�����룬��
��2t�����룬��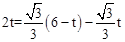 �����
�����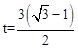 ��������
��������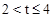 ��
��
iii��E1E2��FF2����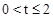 ʱ��ͬһֱ���ϣ��ʵ�
ʱ��ͬһֱ���ϣ��ʵ�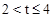 ʱE1E2��FF2��������ͬһֱ���ϡ�
ʱE1E2��FF2��������ͬһֱ���ϡ�
��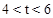 ʱ�����������۵Ľ������AE1E2��һ�����AF1F2��ijһ�߲�������ͬһֱ���ϡ�
ʱ�����������۵Ľ������AE1E2��һ�����AF1F2��ijһ�߲�������ͬһֱ���ϡ�
��������������AE1E2��һ�����AF1F2��ijһ����ͬһֱ����ʱ��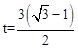 ��
��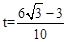 ��t=3��
��t=3��
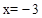 ����ON=3��
����ON=3����
 ����NM=9����M����3����9����
����NM=9����M����3����9��������������C�Ľ���ʽΪ
 ��
����������C����ԭ�㣬��
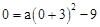 ����
����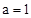 ��
����������C�Ľ���ʽΪ
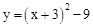 ����
���� ��
����2���١�������
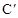 ��������C��ԭ��O��ת1800�õ���
��������C��ԭ��O��ת1800�õ�����������
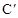 ��������C����ԭ��O�Գơ���������
��������C����ԭ��O�Գơ���������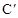 �Ķ�������Ϊ��3��9����
�Ķ�������Ϊ��3��9������������
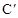 �Ľ���ʽΪ
�Ľ���ʽΪ ����
����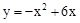 ��
������y=0����x=0��x=6����A��6��0����
�֡�BΪ������
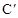 �Ϻ�����Ϊ2�ĵ㣬����x=2����y=8����B��2��8����
�Ϻ�����Ϊ2�ĵ㣬����x=2����y=8����B��2��8������ֱ��AB�Ľ���ʽΪy=kx+b��
��
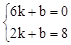 ����ã�
����ã�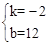 ��
����ֱ��AB�Ľ���ʽΪ
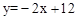 ��
����PΪ�߶�AB��һ���㣬����P
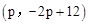 ��
����
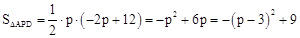 ��
��APD��������ֵΪ9��
����ͼ���ֱ��E2��F2��x��Ĵ��ߣ�����ֱ�ΪG��H��

����ֱ��OB��
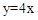 ���ɢ�ֱ��AB��
���ɢ�ֱ��AB��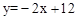 ��
����
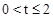 ʱ��E1��OB�ϣ�F1��AB�ϣ�
ʱ��E1��OB�ϣ�F1��AB�ϣ�OE=t��EE1=4t��EG=
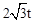 ��OG=
��OG=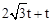 ��GE2=2t��
��GE2=2t��OF=
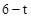 ��FF1=2t��HF=
��FF1=2t��HF=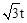 ��OH=
��OH=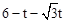 ��HF2= t��
��HF2= t����E��t��0����E1��t��4t����E2��
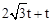 ��2t����F��6��t��0����F1��
��2t����F��6��t��0����F1��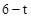 ��2t����F2��
��2t����F2��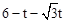 ��t����
��t����i����EE1��FF1��ͬһֱ���ϣ���t=6��t��t=3��������
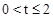 ��
��ii����EE2��F1F2��ͬһֱ���ϣ������EE2��
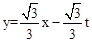 ����F1��
����F1��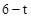 ��2t�����룬��
��2t�����룬��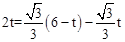 �����
�����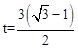 ��
��iii����E1E2��FF2��ͬһֱ���ϣ������E1E2��
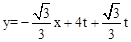 ����F��
����F��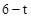 ��0�����룬��
��0�����룬��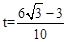 ��
����
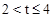 ʱ��E1��F1����AB�ϣ�
ʱ��E1��F1����AB�ϣ�OE=t��EE1=
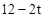 ��EG=
��EG=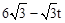 ��OG=
��OG=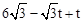 ��GE2=
��GE2=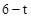 ��
��OF=
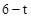 ��FF1=2t��HF=
��FF1=2t��HF=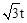 ��OH=
��OH=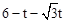 ��HF2= t��
��HF2= t����E��t��0����E1��t��
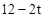 ����E2��
����E2��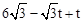 ��
��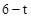 ����F��
����F��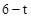 ��0����F1��
��0����F1��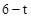 ��2t����F2��
��2t����F2��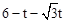 ��t����
��t����i����EE1��FF1��ͬһֱ���ϣ���t=6��t��t=3��
ii����EE2��F1F2��ͬһֱ���ϣ������EE2��
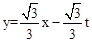 ����F1��
����F1��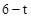 ��2t�����룬��
��2t�����룬��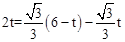 �����
�����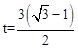 ��������
��������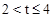 ��
��iii��E1E2��FF2����
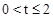 ʱ��ͬһֱ���ϣ��ʵ�
ʱ��ͬһֱ���ϣ��ʵ�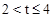 ʱE1E2��FF2��������ͬһֱ���ϡ�
ʱE1E2��FF2��������ͬһֱ���ϡ���
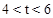 ʱ�����������۵Ľ������AE1E2��һ�����AF1F2��ijһ�߲�������ͬһֱ���ϡ�
ʱ�����������۵Ľ������AE1E2��һ�����AF1F2��ijһ�߲�������ͬһֱ���ϡ���������������AE1E2��һ�����AF1F2��ijһ����ͬһֱ����ʱ��
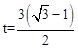 ��
��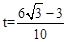 ��t=3��
��t=3����1������ �������M�����꣬���ô���ϵ����������κ�������ʽ���ɡ�
�������M�����꣬���ô���ϵ����������κ�������ʽ���ɡ�
��2���������APD������ڵ�P������ĺ�����ϵʽ��Ӧ�ö��κ�������ֵԭ����⡣
�ڷ�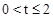 ��
��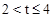 ��
��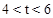 ����������ۣ�ÿ������ַ�EE1��FF1��ͬһֱ���ϣ�EE2��F1F2��ͬһֱ�ߺ�E1E2��FF2��ͬһֱ��������������ۡ�
����������ۣ�ÿ������ַ�EE1��FF1��ͬһֱ���ϣ�EE2��F1F2��ͬһֱ�ߺ�E1E2��FF2��ͬһֱ��������������ۡ�
 �������M�����꣬���ô���ϵ����������κ�������ʽ���ɡ�
�������M�����꣬���ô���ϵ����������κ�������ʽ���ɡ���2���������APD������ڵ�P������ĺ�����ϵʽ��Ӧ�ö��κ�������ֵԭ����⡣
�ڷ�
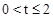 ��
��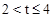 ��
�� ����������ۣ�ÿ������ַ�EE1��FF1��ͬһֱ���ϣ�EE2��F1F2��ͬһֱ�ߺ�E1E2��FF2��ͬһֱ��������������ۡ�
����������ۣ�ÿ������ַ�EE1��FF1��ͬһֱ���ϣ�EE2��F1F2��ͬһֱ�ߺ�E1E2��FF2��ͬһֱ��������������ۡ�
��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 (ǧ��/ʱ)
(ǧ��/ʱ) (��)
(��)

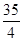
 ��Ϊ������꣬����ͼ��ʾ������ϵ�л���ɲ������
��Ϊ������꣬����ͼ��ʾ������ϵ�л���ɲ������
 ������������ٶȷ��������ײԭ��
������������ٶȷ��������ײԭ�� 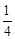 ������������C1����ƽ��h����λ��h��0���õ�������C2��һ��ƽ����x���ֱ�������������߽���A��B��C��D�ĵ㣨��ͼ�����ҵ�A��C����y��Գƣ�ֱ��AB��x��ľ�����m2��m��0����
������������C1����ƽ��h����λ��h��0���õ�������C2��һ��ƽ����x���ֱ�������������߽���A��B��C��D�ĵ㣨��ͼ�����ҵ�A��C����y��Գƣ�ֱ��AB��x��ľ�����m2��m��0����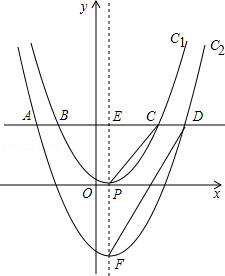
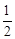 ��
�� ��ֱ��
��ֱ�� ���ڵ�O��0��0����
���ڵ�O��0��0���� ����B����������O��A֮���һ�����㣬����B�ֱ������ᡢ�����ƽ������ֱ��OA���ڵ�C��E��
����B����������O��A֮���һ�����㣬����B�ֱ������ᡢ�����ƽ������ֱ��OA���ڵ�C��E��
 �У���OΪԭ�㣬��B�ڷ���������
�У���OΪԭ�㣬��B�ڷ��������� ��
��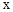 ��
��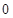 ��ͼ���ϣ���BOC�����Ϊ
��ͼ���ϣ���BOC�����Ϊ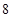 ��
��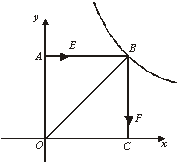
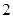 ����λ���ٶ��˶���������һ�����㵽��˵�ʱ����һ��������ֹ֮ͣ�˶������˶�ʱ����t��ʾ����BEF�������
����λ���ٶ��˶���������һ�����㵽��˵�ʱ����һ��������ֹ֮ͣ�˶������˶�ʱ����t��ʾ����BEF�������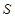 ��ʾ�����S����t�ĺ�����ϵʽ����������˶�ʱ��tȡ��ֵʱ����BEF��������
��ʾ�����S����t�ĺ�����ϵʽ����������˶�ʱ��tȡ��ֵʱ����BEF��������  ��ʱ�������������Ƿ���ڵ�P��ʹ��PEF���ܳ���С�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��ʱ�������������Ƿ���ڵ�P��ʹ��PEF���ܳ���С�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ� ��ͼ����ͼ��ʾ�������н��ۣ�
��ͼ����ͼ��ʾ�������н��ۣ� ����
���� ����
���� ����
����  ����
����
 ��ͼ����ͼ��ʾ������˵���в���ȷ���ǡ� ��
��ͼ����ͼ��ʾ������˵���в���ȷ���ǡ� ��