题目内容
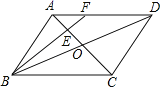
【题目】如图,平行四边形ABCD中,AC、BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,S△AEF=4,则下列结论:①FD=2AF;②S△BCE=36;③S△ABE=16; ④△AEF∽△ACD,其中一定正确的是( )
A.①②④B.①②③C.②③④D.①②
【答案】D
【解析】
①根据四边形ABCD是平行四边形,可得OA=OC,AD∥BC,AD=BC,由点E是OA的中点,可得CE=3AE,再根据相似三角形对应边成比例即可判断;
②根据相似三角形的面积比等于相似比的平方即可判断;
③根据等高的两个三角形面积的比等于底与底的比即可求出三角形ABE的面积;
④假设△AEF∽△ACD,可得EF∥CD,即BF∥CD,由已知AB∥CD,可得BF和AB共线,由点E是OA的中点,即BE与AB不共线,得假设不成立,即△AEF和△ACD不相似,即可判断.
解:①∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,AD=BC,
∵点E是OA的中点,
∴CE=3AE,
∵AF∥BC,
∴△AEF∽△CEB,
∴![]() ,
,
∴BC=3AF,
∴FD=2AF,
所以结论①正确;
②∵△AEF∽△CEB,
CE=3AE,
∴![]() ,
,
∴S△BCE=9S△FAE=36,
所以结论②正确;
③∵△ABE和△CBE等高,且BE=3AE,
∴S△BCE=3S△ABE,
∴S△ABE=12,
所以结论③错误;
④假设△AEF∽△ACD,
∴EF∥CD,即BF∥CD,
∵AB∥CD,
∴BF和AB共线,
∵点E是OA的中点,即BE与AB不共线,
∴假设不成立,即△AEF和△ACD不相似,
所以结论④错误.
综上所述:正确的结论有①②.
故选:D.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案【题目】某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制例图1、图2两幅均不完整的统计图表.
校本课程 | 频数 | 频率 |
A | 36 | 0.45 |
B |
| 0.25 |
C | 16 | b |
D | 8 |
|
合计 | a | 1 |
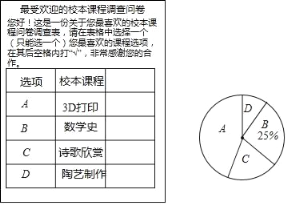
请您根据图表中提供的信息回答下列问题:
(1)统计表中的a= ,b= ;
(2)“D”对应扇形的圆心角为 度;
(3)根据调查结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数;
(4)小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.