题目内容
【题目】已知∠AOB=45°,点P在∠AOB内部,P1与P关于OB对称,P2与P关于OA对称,则P1 , O,P2三点构成的三角形是( )
A.直角三角形
B.等腰三角形
C.等边三角形
D.等腰直角三角形
【答案】D
【解析】解:如图,连接OP,
∵P1与P关于OB对称,P2与P关于OA对称,
∴OP=OP1=OP2 , ∠BOP1=∠BOP,∠AOP2=∠AOP,
∴∠P1OP2=∠BOP1+∠BOP+∠AOP2+∠AOP=2(∠BOP+∠AOP)=2∠AOB,
∵∠AOB=45°,
∴∠P1OP2=2×45°=90°,
∴P1 , O,P2三点构成的三角形是等腰直角三角形.
所以答案是:D.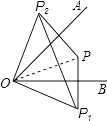
【考点精析】根据题目的已知条件,利用轴对称的性质的相关知识可以得到问题的答案,需要掌握关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目