题目内容
【题目】如图,在锐角三角形ABC中,BC=4![]() ,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,试求CM+MN的最小值.
,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,试求CM+MN的最小值.

【答案】CM+MN的最小值为4.
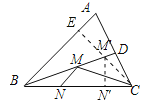
【解析】试题分析:过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC于N′,则CE即为CM+MN的最小值,再根据∠ABC=45°,CE⊥AB,可知△BCE是等腰直角三角形,由锐角三角函数的定义即可求出CE的长.
试题解析:
过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC于N′,则CE即为CM+MN的最小值,
∵BC=4![]() ,∠ABC=45°,CE⊥AB,
,∠ABC=45°,CE⊥AB,
∴△BCE是等腰直角三角形,
∴CE=BCcos45°=4![]() ×
×![]() =4.
=4.
故CM+MN的最小值为4.

练习册系列答案
相关题目