题目内容
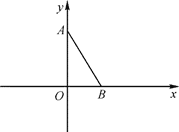
【题目】如图1,点O是直线AB上的一点.
(1)如图1,当∠AOD是直角,3∠AOC=∠BOD,求∠COD的度数;
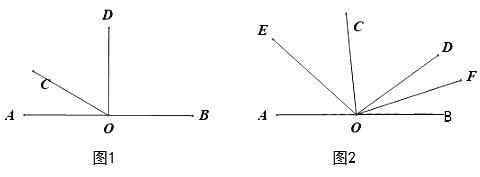
(2)在(1)中∠COD绕着点O顺时针旋转(OD与OB重合即停止),如图2,OE、OF分别平分∠AOC、∠BOD,则在旋转过程中∠EOF的大小是否变化?若不变,求出∠EOF的大小;若改变,说明理由;
(3)在(1)中线段OC、OD绕着点O顺时针旋转,速度分别为每秒20°和每秒10°(当OD与OB重合时旋转都停止),OM、ON分别平分∠BOC、∠BOD,多少秒时∠COM=∠BON(直接写出答案,不必写出过程).
【答案】(1)60°;(2)120°;(3)6秒.
【解析】
(1)根据直角的定义求出∠BOD,再根据3∠AOC=∠BOD可得∠AOC的度数,又因为∠COD与∠AOC 互余即可解答;
(2)不变,是120°.根据(1)求出∠COD的度数,从而求得∠AOC+∠BOD的值, 再利用角平分线定义求出∠EOC +∠DOF,最后根据∠EOF=∠EOC +∠DOF+∠COD即可解答.
(3) 设t秒时,∠COM=∠BON.用含t的式子表示出∠COM、∠BON,从而列出方程求解.
解:(1)因为∠AOD是直角,所以∠AOD= =90°,又因为3∠AOC=∠BOD,所以∠AOC=![]() ∠BOD=30°,所以∠COD=∠AOD-∠AOC=90°-30°=60°;
∠BOD=30°,所以∠COD=∠AOD-∠AOC=90°-30°=60°;
(2)因为∠AOD是直角,∠AOC=30°,所以∠COD=∠AOD-∠AOC=90°-30°=60°,
所以∠AOC+∠BOD=180°-∠COD=180°- 60°=120°,因为OE、OF分别平分∠AOC、∠BOD,所以∠EOC +∠DOF =![]() (∠AOC+∠BOD)=×120°=60°,所以∠EOF=∠EOC +∠DOF+∠COD=60°+60°=120°;
(∠AOC+∠BOD)=×120°=60°,所以∠EOF=∠EOC +∠DOF+∠COD=60°+60°=120°;
(3)设t秒时,∠COM=∠BON.t秒时,∠COM=![]() (180°-∠AOC-20°t)=
(180°-∠AOC-20°t)= ![]() (180°-30°-20°t)=75°-10°t,∠BON=
(180°-30°-20°t)=75°-10°t,∠BON=![]() ∠BOD=
∠BOD=![]() (90°-10°t)=45°-5°t,当∠COM=∠BON时,75°-10°t=45°-5°t,解得:t=6,即6s时,∠COM=∠BON.
(90°-10°t)=45°-5°t,当∠COM=∠BON时,75°-10°t=45°-5°t,解得:t=6,即6s时,∠COM=∠BON.

【题目】在如图中,每个正方形由边长为1的小正方形组成: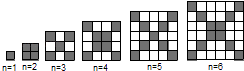
(1)观察图形,请填写下列表格:
正方形边长 | 1 | 3 | 5 | 7 | … | n(奇数) |
黑色小正方形个数 |
正方形边长 | 2 | 4 | 6 | 8 | … | n(偶数) |
黑色小正方形个数 |
(2)在边长为n(n≥1)的正方形中,设黑色小正方形的个数为P1 , 白色小正方形的个数为P2 , 问是否存在偶数n,使P2=5P1?若存在,请写出n的值;若不存在,请说明理由.