题目内容
【题目】“新禧”杂货店去批发市场购买某种新型儿童玩具，第一次用1200元购得玩具若干个，并以7元的价格出售，很快就售完．由于该玩具深受儿童喜爱，第二次进货时每个玩具的批发价已比第一次提高了20%，他用1500元所购买的玩具数量比第一次多10个，再按8元售完，问该老板两次一共赚了多少钱？
【答案】解：设这种新型儿童玩具第一次进价为x元/个，则第二次进价为1.2x元/个， 根据题意，得 
﹣ 
=10，
变形为：1500﹣1440=12x，
解得：x=5，
经检验，x=5是原方程的解，
则该老板这两次购买玩具一共盈利为： 
（7﹣1.2×5）+ 
×（7﹣5）=730（元）．
答：该老板两次一共赚了730元
【解析】设这种新型儿童玩具第一次进价为x元/个，则第二次进价为1.2x元/个，分别可以表示出第一次购买玩具的数量和第二次购买玩具的数量，根据两次购买玩具的数量之间的关系建立方程求出其解就可以了．
【考点精析】通过灵活运用分式方程的应用，掌握列分式方程解应用题的步骤：审题、设未知数、找相等关系列方程、解方程并验根、写出答案（要有单位）即可以解答此题．
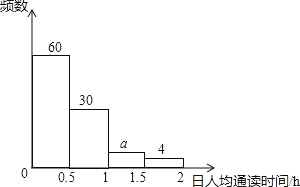
阅读快车系列答案
【题目】某校1200名学生参加了全区组织的“经典诵读”活动，该校随机选取部分学生，对他们在三、四两个月的诵读时间进行调查，下面是根据调查数据制作的统计图表的一部分．
根据以上信息，解答下列问题：
（1）本次调查的学生数为 人；
（2）图表中的a、b、c的值分别为 ， ， ；
（3）在被调查的学生中，四月份日人均诵读时间在1＜x≤1.5范围内的人数比三月份在此范围的人数多 人；
（4）试估计该校学生四月份人均诵读时间在1小时以上的人数．
四月日人均诵读时间的统计表
日人均诵读时间x/h | 人数 | 百分比 |
0≤x≤0.5 | 6 | |
0.5＜x≤1 | 30 | |
1＜x≤1.5 | 50% | |
1.5＜x≤2 | 10 | 10% |
2＜x≤2.5 | b | c |
三月日人均诵读时间的频数分布直方图
