题目内容
【题目】已知△ABC是等边三角形.
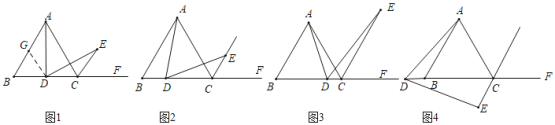
(1)如图1,点D是边BC的中点,∠ADE=60°,且DE交△ABC外角∠ACF的平分线CE于点E,求证:AD=DE;(提示:取AB的中点G,连接DG)
(2)小颖对(1)题进行了探索:如果将(1)题中的“点D是边BC的中点”改为“点D是直线BC上任意一点(B、C两点除外)”,其它条件不变,结论AD=DE是否仍然成立?小颖将点D的位置分为三种情形,画出了图2、图3、图4,现在请你在图2、图3、图4中选择一种情形,帮小颖验证:结论AD=DE是否仍然成立?
【答案】(1)证明见解析;(2)成立,证明见解析.
【解析】
(1)取AB的中点G,连接DG,根据“ASA”证明△AGD≌△DCE即可;
(2)小颖的观点正确.如图2中,在AB上取一点M,使BM=BD,连接MD.如图3中,延长BA到M,使AM=CD,利用全等三角形的性质解决问题即可.
解:(1)取AB的中点G,连接DG,
∵△ABC是等边三角形,
∴∠BAC=∠B=∠ACB=60°,BA=BC=AC,AD⊥BC,
∴CD=![]() ,∠BAD=30°,
,∠BAD=30°,
∵G是AB中点,
∴AG=DG=![]() ,
,
∴AG=CD, △BGD是等边三角形,∠BGD=60°,∠AGD=120°.
∵∠ADE=60°,
∴∠CDE=30°,
∴∠GAD=∠CDE.
∵CE是外角∠ACF的平分线,
∴∠ECA=60°,
∴∠DCE=120°.
∴∠AGD=∠DCE.
在△AGD和△DCE中,
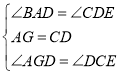 ,
,
∴△AGD≌△DCE(ASA).
∴AD=DE.
(2)小颖的观点正确.
证明:如图2中,在AB上取一点M,使BM=BD,连接MD.
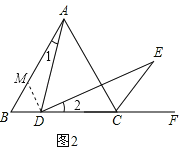
∵△ABC是等边三角形,
∴∠B=60°,BA=BC.
∴△BMD是等边三角形,∠BMD=60°.∠AMD=120°.
∵CE是外角∠ACF的平分线,
∴∠ECA=60°,∠DCE=120°.
∴∠AMD=∠DCE.
∵∠ADE=∠B=60°,∠ADC=∠2+∠ADE=∠1+∠B
∴∠1=∠2.
又∵BA﹣BM=BC﹣BD,即MA=CD.
在△AMD和△DCE中,
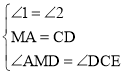 ,
,
∴△AMD≌△DCE(ASA).
∴AD=DE.
如图3中,延长BA到M,使AM=CD,
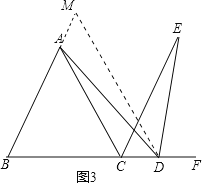
与(1)相同,可证△BDM是等边三角形,
∵∠CDE=∠ADB+∠ADE=∠ADB+60°,
∠MAD=∠B+∠ADB=∠ADB+60°,
∴∠CDE=∠MAD,
同理可证,△AMD≌△DCE,
∴AD=DE.
如图4中,同法可证AD=DE.