��Ŀ����
��֪����ͼ���ı���ABCD�ǵ������Σ�����AD��BC��AD=2��BC=4��AB=DC=2����M�ӵ�B��ʼ����ÿ��1����λ���ٶ����C�˶�����N�ӵ�D��ʼ����D��A��B������ÿ��1����λ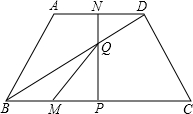 ���ٶ����B�˶�������M��Nͬʱ��ʼ�˶�������һ�㵽���յ㣬��һ��Ҳֹͣ�˶����˶�ʱ��Ϊt��t��0��������N��NP��BC��P����BD�ڵ�Q��
���ٶ����B�˶�������M��Nͬʱ��ʼ�˶�������һ�㵽���յ㣬��һ��Ҳֹͣ�˶����˶�ʱ��Ϊt��t��0��������N��NP��BC��P����BD�ڵ�Q����1����D��BC�ľ���Ϊ
��2�����tΪ��ֵʱ��QM��AB��
��3�����BMQ�����ΪS����S��t�ĺ�����ϵʽ��
��4�����tΪ��ֵʱ����BMQΪֱ�������Σ�
��������1���ֱ����A��D��BC���ϵĸߣ���BC����E��F�������ı���ABCD�ǵ������Σ��ɵó�BE=CF=��BC-AD����2=1������AB=DC=2�����ݹ��ɶ����ɵõ�D��BC�ľ���DF=
=
��2�����ݣ�1���ó���DF��ֵ�������BD�ij�Ϊ2
����ô������BDC�Ǹ�ֱ�������Σ��ҡ�C=60�㣬��DBC=30�㣬���QM��AB���ɵó���PMQ����Ҳ��60�㣬���ȱ�ʾ��MP�ij���Ȼ����ݡ�PQM�Ķ�����ʾ��PQ��Ȼ�����QP��DF���ó�����QP��DF��BP��BF�ı�����ϵʽ��DF��ֵ�Ƕ�ֵ���ɱ�ʾ��BP��BF�������Ϳ����t��ֵ��
��3��Ҫ�����������������
�ٵ�N��AD��ʱ���ؼ������PQ������ֱ��������BPQ�У��ȱ�ʾ��BP��Ȼ����ݡ�QBP�Ķ����������PQ�ij���Ȼ����������ε������ʽ���ɵó�S��t�ĺ�����ϵʽ��
��N��AB��ʱ������Ҫ�����PQ��ֵ�����ȱ�ʾ��BN��Ȼ����ֱ��������BNP�У���ʾ��BP��������ֱ��������BPQ�У���BP��ʾ��PQ�����ɸ��������ε������ʽ�ó�S��t�ĺ�����ϵʽ��
��4��ҲҪ����������������ۣ�
��һ���������N��AD��ʱ���ٵ���BMQ=90��ʱ����ôM��P�غϣ����Ǿ���BM+ND+FC=BC����2t+1=4�����ɵó�t��ֵ��
�ڵ���BQM=90��ʱ��������ֱ��������NDQ�У���ND�ij�����ʾ��NQ��Ȼ����������D��BC�ľ��룬���ɱ�ʾ��PQ����ʱPQ�ĵ�һ�ֱ�ʾ�������ڶ��ֱ�ʾ�����ǣ���ֱ��������BMQ�У���BM��ʾ��QM��Ȼ����ֱ��������QPM�У���ʾ��PQ��Ȼ�������������ʾPQ��ʽ����ȣ����ɵó���ʱ��t��ֵ��
�ڶ����������N��AB��ʱ����ʱֻ�С�BQM=90�㣬����ͬ�ڣ�Ҳ��ͨ����ͬ�ı�ʾPQ�ķ������ó�t��ֵ������ͬ��3���ڣ�
| 22-1 |
| 3 |
��2�����ݣ�1���ó���DF��ֵ�������BD�ij�Ϊ2
| 3 |
��3��Ҫ�����������������
�ٵ�N��AD��ʱ���ؼ������PQ������ֱ��������BPQ�У��ȱ�ʾ��BP��Ȼ����ݡ�QBP�Ķ����������PQ�ij���Ȼ����������ε������ʽ���ɵó�S��t�ĺ�����ϵʽ��
��N��AB��ʱ������Ҫ�����PQ��ֵ�����ȱ�ʾ��BN��Ȼ����ֱ��������BNP�У���ʾ��BP��������ֱ��������BPQ�У���BP��ʾ��PQ�����ɸ��������ε������ʽ�ó�S��t�ĺ�����ϵʽ��
��4��ҲҪ����������������ۣ�
��һ���������N��AD��ʱ���ٵ���BMQ=90��ʱ����ôM��P�غϣ����Ǿ���BM+ND+FC=BC����2t+1=4�����ɵó�t��ֵ��
�ڵ���BQM=90��ʱ��������ֱ��������NDQ�У���ND�ij�����ʾ��NQ��Ȼ����������D��BC�ľ��룬���ɱ�ʾ��PQ����ʱPQ�ĵ�һ�ֱ�ʾ�������ڶ��ֱ�ʾ�����ǣ���ֱ��������BMQ�У���BM��ʾ��QM��Ȼ����ֱ��������QPM�У���ʾ��PQ��Ȼ�������������ʾPQ��ʽ����ȣ����ɵó���ʱ��t��ֵ��
�ڶ����������N��AB��ʱ����ʱֻ�С�BQM=90�㣬����ͬ�ڣ�Ҳ��ͨ����ͬ�ı�ʾPQ�ķ������ó�t��ֵ������ͬ��3���ڣ�
����⣺��1��
��2����A��AE��BC��E����D��DF��BC��F�����ı���AEFD�Ǿ��Σ�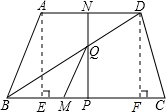
BE=CF=
=1��
ֱ��������CFD�У�CF=1��CD=2��cos��C=
���C=60�㣬DF=
��
���ABE=��C=60��
��QM��AB
���QMP=60��
��BM=t��PF=ND=t��FC=1��BC=4
��PM=3-2t��BP=3-t��
ֱ��������QPM�У���QMP=60�㣬PM=3-2t��QP=
��3-2t����
��QP��BC��DF��BC
��QP��DF��
���BQP�ס�BDF��
��
=
����
=
��5t=6����t=1.2��s��
��t=1.2sʱ��QM��AB
��3����0��t��2ʱ��������BDF�У�BF=3��DF=
��
��BD=2
������BCD��CD=2��BD=2
��BC=4��
���BD2+CD2=BC2��
��������BDC��ֱ�������Σ��ҡ�BDC=90�㣬��DBC=30�㣮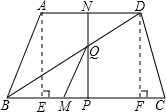
ֱ��������BQP�У�BP=3-t����DBC=30�㣬
��PQ=
��3-t��
��ˣ�S=
��t��
��3-t��=-
t2+
t
��2��t��4ʱ��ֱ��������NBP�У���ABC=60�㣬BN=4-t��
��BP=
��
��ֱ��������BPQ�У���DBC=30�㣬BP=
��
��QP=
��ˣ�S=
��t��
=-
t2+
t
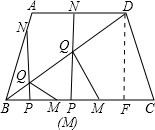
��4����0��t��2ʱ����N��AD��ʱ������������������ۣ�
�ٵ���BMQ=90�㣬��M��P���غϣ���ôBM+PF+CF=BM+ND+CF=2t+1=4
��ã�t=1.5s��
�ڵ���BQM=90�㣬��ֱ��������NQD�У�ND=t����ADB=��DBC=30�㣬
��NQ=
t��
��NP=
��QP=
-
t
��ֱ��������BQM�У���DBC=30�㣬BM=t
��QM=
t
��ֱ��������QPM�У���QMP=60�㣬QM=
t
��QP=
t
��
-
t=
t��
���t=
s��
��2��t��4ʱ����BQM=90��
ֱ��������BNP�У�BN=4-t����ABC=60�㣬
��BP=
��
��PM=BM-BP=t-
=
��ֱ��������BPQ�У���DBC=30�㣬BP=
��PQ=
ֱ��������QPM�У���QMP=60�㣬PM=
��PQ=
���
=
��
���t=1.6s�����ʱt��ȡֵ��Χ������
������������������
������������t=1.5s��
s����BMQ��ֱ�������Σ�
| 3 |
��2����A��AE��BC��E����D��DF��BC��F�����ı���AEFD�Ǿ��Σ�

BE=CF=
| BC-AD |
| 2 |
ֱ��������CFD�У�CF=1��CD=2��cos��C=
| 1 |
| 2 |
���C=60�㣬DF=
| 3 |
���ABE=��C=60��
��QM��AB
���QMP=60��
��BM=t��PF=ND=t��FC=1��BC=4
��PM=3-2t��BP=3-t��
ֱ��������QPM�У���QMP=60�㣬PM=3-2t��QP=
| 3 |
��QP��BC��DF��BC
��QP��DF��
���BQP�ס�BDF��
��
| BP |
| BF |
| QP |
| DF |
| 3-t |
| 3 |
| ||
|
��5t=6����t=1.2��s��
��t=1.2sʱ��QM��AB
��3����0��t��2ʱ��������BDF�У�BF=3��DF=
| 3 |
��BD=2
| 3 |
������BCD��CD=2��BD=2
| 3 |
���BD2+CD2=BC2��
��������BDC��ֱ�������Σ��ҡ�BDC=90�㣬��DBC=30�㣮

ֱ��������BQP�У�BP=3-t����DBC=30�㣬
��PQ=
| ||
| 3 |
��ˣ�S=
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
| ||
| 2 |
��2��t��4ʱ��ֱ��������NBP�У���ABC=60�㣬BN=4-t��
��BP=
| 4-t |
| 2 |
��ֱ��������BPQ�У���DBC=30�㣬BP=
| 4-t |
| 2 |
��QP=
| ||
| 6 |
��ˣ�S=
| 1 |
| 2 |
| ||
| 6 |
| ||
| 12 |
| ||
| 3 |

��4����0��t��2ʱ����N��AD��ʱ������������������ۣ�
�ٵ���BMQ=90�㣬��M��P���غϣ���ôBM+PF+CF=BM+ND+CF=2t+1=4
��ã�t=1.5s��
�ڵ���BQM=90�㣬��ֱ��������NQD�У�ND=t����ADB=��DBC=30�㣬
��NQ=
| ||
| 3 |
��NP=
| 3 |
��QP=
| 3 |
| ||
| 3 |
��ֱ��������BQM�У���DBC=30�㣬BM=t
��QM=
| 1 |
| 2 |
��ֱ��������QPM�У���QMP=60�㣬QM=
| 1 |
| 2 |
��QP=
| ||
| 4 |
��
| 3 |
| ||
| 3 |
| ||
| 4 |
���t=
| 12 |
| 7 |
��2��t��4ʱ����BQM=90��
ֱ��������BNP�У�BN=4-t����ABC=60�㣬
��BP=
| 4-t |
| 2 |
��PM=BM-BP=t-
| 4-t |
| 2 |
| 3t-4 |
| 2 |
��ֱ��������BPQ�У���DBC=30�㣬BP=
| 4-t |
| 2 |
��PQ=
| ||
| 6 |
ֱ��������QPM�У���QMP=60�㣬PM=
| 3t-4 |
| 2 |
��PQ=
| ||
| 2 |
���
| ||
| 6 |
| ||
| 2 |
���t=1.6s�����ʱt��ȡֵ��Χ������
������������������
������������t=1.5s��
| 12 |
| 7 |
������������Ҫ�����˵������ε����ʣ����������ε����ʵ�֪ʶ�㣬Ҫע����ǣ�3����4����Ҫ��������ۣ���Ҫ©�⣮

��ϰ��ϵ�д�
 �ǻۿ����ܾ�100�ֵ�Ԫ���ؼ��ϵ�д�
�ǻۿ����ܾ�100�ֵ�Ԫ���ؼ��ϵ�д� ��Ԫ������ĩ��ϵ�д�
��Ԫ������ĩ��ϵ�д�
�����Ŀ
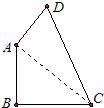 ��֪����ͼ���ı���ABCD�С�B=90�㣬AB=9��BC=12��AD=8��CD=17��
��֪����ͼ���ı���ABCD�С�B=90�㣬AB=9��BC=12��AD=8��CD=17��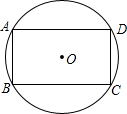 ��֪����ͼ���ı���ABCD�ڽ��ڡ�O����AB��CD��AD��BC��
��֪����ͼ���ı���ABCD�ڽ��ڡ�O����AB��CD��AD��BC�� ��֪����ͼ���ı���ABCD�������Σ�E��F�ֱ���AB��AD�ӳ����ϵĵ㣬��BE=DF
��֪����ͼ���ı���ABCD�������Σ�E��F�ֱ���AB��AD�ӳ����ϵĵ㣬��BE=DF ��֪����ͼ���ı���ABCD�У�BC=CD=10��AB=15��AB��BC��CD��BC�������ı���ABCD��ֱ��AB��תһ�ܣ������ü�����ı�����Ƕ��٣�
��֪����ͼ���ı���ABCD�У�BC=CD=10��AB=15��AB��BC��CD��BC�������ı���ABCD��ֱ��AB��תһ�ܣ������ü�����ı�����Ƕ��٣� ��֪����ͼ���ı���ABCD��һ��P��
��֪����ͼ���ı���ABCD��һ��P��